题目内容
15．已知函数f（x）=x（x-1）（x-2），x∈（0，2），点P（x，y）是函数f（x）图象上任一点，其中O（0，0），A（2，0），记△OAP的面积为g（x），则g′（x）的图象可能是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 先利用图象确定△OAP的面积为g（x），然后利用导数求出g'（x），然后确定函数g'（x）的图象
解答 解：画出f（x）=x（x-1）（x-2），x∈（0，2）的图象，如图所示，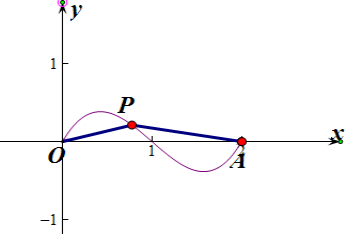
当0＜x＜1时，g（x）=x（x-1）（x-2），
∴g′（x）=3x2-6x+2=3（x-1）2-1
当x=1时，g（x）不存在．
当1＜x＜2时，g（x）=-x（x-1）（x-2），
∴g′（x）=-3x2+6x-2=-3（x-1）2+1，
故g'（x）的图象可能是B
故选：B．
点评 本题主要考查了函数的导数运算以及函数图象的判断和识别，先通过条件确定函数g（x）的表达式是解决本题的关键，属于中档题．
练习册系列答案
相关题目
5．若向量$\overrightarrow{m}$=（1，2），$\overrightarrow{n}$=（x，1）满足$\overrightarrow{m}$⊥$\overrightarrow{n}$，则|$\overrightarrow{n}$|=（ ）
| A． | $\frac{\sqrt{5}}{4}$ | B． | $\frac{\sqrt{5}}{2}$ | C． | $\sqrt{5}$ | D． | 5 |
若复数t=$\frac{2}{（1-i）^{2}}$+$\frac{3+i}{1-i}$的虚部为m，函数f（x）=x+$\frac{4}{x-1}$+1，（x∈{2，3}）的最小值为n．
4．盒子中分别有红球3个、白球2个、黑球1个，共6个球，从中任意取出两个球，则与事件“至少有一个白球”互斥而不对立的事件是（ ）
| A． | 都是白球 | B． | 至少有一个红球 | C． | 至少有一个黑球 | D． | 红、黑球各一个 |
5．将正整数1，2，3，4，5随机分成甲乙两组，使得每组至少有一个数，则每组中各数之和是3的倍数的概率是（ ）
| A． | $\frac{2}{21}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{2}{5}$ |