题目内容
某银行的一个营业窗口可办理四类业务,假设顾客办理业务所需的时间互相独立,且都是整数分钟,经统计以往100位顾客办理业务所需的时间(t),结果如下:
| 类别 | A类 | B类 | C类 | D类 |
| 顾客数(人) | 20 | 30 | 40 | 10 |
| 时间t(分钟/人) | 2 | 3 | 4 | 6 |
(Ⅰ)求银行工作人员恰好在第6分钟开始办理第三位顾客的业务的概率;
(Ⅱ)用X表示至第4分钟末已办理完业务的顾客人数,求X的分布列及数学期望.
解:(Ⅰ)设Y表示银行工作人员办理业务需要的时间,用频率估计概率得Y的分布列如下:
用A表示事件“银行工作人员恰好在第6分钟开始办理第三位顾客的业务”,则事件A有两种情形:
①办理第一位业务所需的时间为2分钟,且办理第二位业务所需的时间为3分钟;
②办理第一位业务所需的时间为3分钟,且办理第二位业务所需的时间为2分钟;
∴P(A)=P(Y=2)P(Y=3)+P(Y=3)P(Y=2)=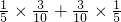 =
=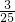 ;
;
(Ⅱ)由题意可知X的取值为0,1,2,
X=0对应办理第一位的业务需时超过4分钟,故P(X=0)=P(Y>4)= ,
,
X=1对应办理第一位业务所需的时间为2分钟,且办理第二位业务所需的时间超过分钟,
或办理第一位业务所需的时间为3分钟,或办理第一位业务所需的时间为4分钟,
故P(X=1)=P(Y=2)P(Y>2)+P(Y=3)+P(Y=4)=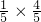 +
+ +
+ =
= ,
,
X=2对应办理两位顾客业务时间均为2分钟,故P(X=2)=P(Y=2)P(Y=2)=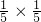 =
= ,
,
故X的分布列为:
故EX=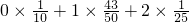 =
=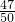
分析:(Ⅰ)设Y表示银行工作人员办理业务需要的时间,用频率估计概率得Y的分布列,用A表示事件“银行工作人员恰好在第6分钟开始办理第三位顾客的业务”,则事件A有两种情形:
①办理第一、二位业务所需的时间分别为2、3分钟;②办理第一、二位业务所需的时间分别为3、2分钟;故P(A)=P(Y=2)P(Y=3)+P(Y=3)P(Y=2),计算可得;
(Ⅱ)由题意可知X的取值为0,1,2,X=0对应办理第一位的业务需时超过4分钟,X=1对应办理第一位业务所需的时间为2分钟,且办理第二位业务所需的时间超过分钟,或办理第一位业务所需的时间为3分钟,或办理第一位业务所需的时间为4分钟,X=2对应办理两位顾客业务时间均为2分钟,分别可得其概率,进而可得分布列和数学期望故EX.
点评:本题考查离散型随机变量及其分布列,涉及数学期望的求解和频率分布表的应用,属中档题.
| Y | 2 | 3 | 4 | 6 |
| P |  |  |  |  |
①办理第一位业务所需的时间为2分钟,且办理第二位业务所需的时间为3分钟;
②办理第一位业务所需的时间为3分钟,且办理第二位业务所需的时间为2分钟;
∴P(A)=P(Y=2)P(Y=3)+P(Y=3)P(Y=2)=
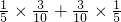 =
=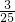 ;
;(Ⅱ)由题意可知X的取值为0,1,2,
X=0对应办理第一位的业务需时超过4分钟,故P(X=0)=P(Y>4)=
 ,
,X=1对应办理第一位业务所需的时间为2分钟,且办理第二位业务所需的时间超过分钟,
或办理第一位业务所需的时间为3分钟,或办理第一位业务所需的时间为4分钟,
故P(X=1)=P(Y=2)P(Y>2)+P(Y=3)+P(Y=4)=
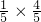 +
+ +
+ =
= ,
,X=2对应办理两位顾客业务时间均为2分钟,故P(X=2)=P(Y=2)P(Y=2)=
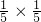 =
= ,
,故X的分布列为:
| X | 0 | 1 | 2 |
| P |  |  |  |
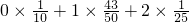 =
=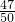
分析:(Ⅰ)设Y表示银行工作人员办理业务需要的时间,用频率估计概率得Y的分布列,用A表示事件“银行工作人员恰好在第6分钟开始办理第三位顾客的业务”,则事件A有两种情形:
①办理第一、二位业务所需的时间分别为2、3分钟;②办理第一、二位业务所需的时间分别为3、2分钟;故P(A)=P(Y=2)P(Y=3)+P(Y=3)P(Y=2),计算可得;
(Ⅱ)由题意可知X的取值为0,1,2,X=0对应办理第一位的业务需时超过4分钟,X=1对应办理第一位业务所需的时间为2分钟,且办理第二位业务所需的时间超过分钟,或办理第一位业务所需的时间为3分钟,或办理第一位业务所需的时间为4分钟,X=2对应办理两位顾客业务时间均为2分钟,分别可得其概率,进而可得分布列和数学期望故EX.
点评:本题考查离散型随机变量及其分布列,涉及数学期望的求解和频率分布表的应用,属中档题.

练习册系列答案
相关题目
某银行的一个营业窗口可办理四类业务,假设顾客办理业务所需的时间互相独立,且都是整数分钟,经统计以往100位顾客办理业务所需的时间(t),结果如下:
注:银行工作人员在办理两项业务时的间隔时间忽略不计,并将频率视为概率.
(Ⅰ)求银行工作人员恰好在第6分钟开始办理第三位顾客的业务的概率;
(Ⅱ)用X表示至第4分钟末已办理完业务的顾客人数,求X的分布列及数学期望.
| 类别 | A类 | B类 | C类 | D类 |
| 顾客数(人) | 20 | 30 | 40 | 10 |
| 时间t(分钟/人) | 2 | 3 | 4 | 6 |
(Ⅰ)求银行工作人员恰好在第6分钟开始办理第三位顾客的业务的概率;
(Ⅱ)用X表示至第4分钟末已办理完业务的顾客人数,求X的分布列及数学期望.
据统计,在某银行的一个营业窗口等候的人数及其相应的概率如下:
排队人数 | 0人 | 1人 | 2人 | 3人 | 4人 | 5人及5人以上 |
概率 | 0.05 | 0.14 | 0.35 | 0.3 | 0.1 | 0.06 |
试求:(1)至多有2人等候排队的概率是多少?
(2)至少有3人等候排队的概率是多少?