题目内容
若指数函数f(x)=ax(a>0且a≠1)的部分对应值如表所示,则下列表述中,正确的是( )| x | -2 |
| f(x) | 0.592 |
A.0<a<1
B.f(x)=ax(a>0且a≠1)的反函数为g(x)=-logax(a>0且a≠1)
C.
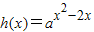 的单调递增区间为(-∞,1]
的单调递增区间为(-∞,1]D.F(x)=ax-a的图象不过第二象限
【答案】分析:由题设知f(x)=ax(a>0且a≠1),且a-2=0.592,故a>1;f(x)=ax(a>0且a≠1)的反函数为g(x)=logax(a>0且a≠1);由a>1,知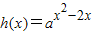 的单调递增区间为[1,+∞),F(x)=ax-a的图象不过第二象限.
的单调递增区间为[1,+∞),F(x)=ax-a的图象不过第二象限.
解答:解:由题设知f(x)=ax(a>0且a≠1),
且a-2=0.592,
∴a>1,故A不正确;
f(x)=ax(a>0且a≠1)的反函数为g(x)=logax(a>0且a≠1),故B不正确;
∵a>1,∴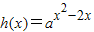 的单调递增区间为[1,+∞),故C不正确;
的单调递增区间为[1,+∞),故C不正确;
∵a>1,∴F(x)=ax-a的图象不过第二象限,故D正确.
故选D.
点评:本题考查命题的真假判断与应用,是基础题.解题时要认真审题,仔细解答,注意指数函数性质的灵活运用.
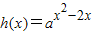 的单调递增区间为[1,+∞),F(x)=ax-a的图象不过第二象限.
的单调递增区间为[1,+∞),F(x)=ax-a的图象不过第二象限.解答:解:由题设知f(x)=ax(a>0且a≠1),
且a-2=0.592,
∴a>1,故A不正确;
f(x)=ax(a>0且a≠1)的反函数为g(x)=logax(a>0且a≠1),故B不正确;
∵a>1,∴
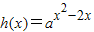 的单调递增区间为[1,+∞),故C不正确;
的单调递增区间为[1,+∞),故C不正确;∵a>1,∴F(x)=ax-a的图象不过第二象限,故D正确.
故选D.
点评:本题考查命题的真假判断与应用,是基础题.解题时要认真审题,仔细解答,注意指数函数性质的灵活运用.

练习册系列答案
相关题目