题目内容
不等式组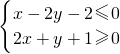 所确定的平面区域为D,则该平面区域D在圆x2+(y+1)2=4内的面积是________.
所确定的平面区域为D,则该平面区域D在圆x2+(y+1)2=4内的面积是________.
π
分析:先依据不等式组组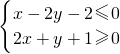 结合二元一次不等式(组)与平面区域的关系画出其表示的平面区域,再利用圆的方程画出图形,最后利用扇形面积公式计算即可.
结合二元一次不等式(组)与平面区域的关系画出其表示的平面区域,再利用圆的方程画出图形,最后利用扇形面积公式计算即可.
解答: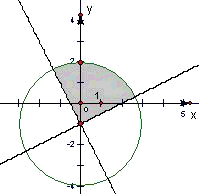 解:如图阴影部分表示
解:如图阴影部分表示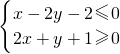 确定的平面区域,所以阴影部分扇形即为所求.
确定的平面区域,所以阴影部分扇形即为所求.
由于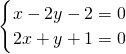 得两直线的交点(0,-1)即为圆心,
得两直线的交点(0,-1)即为圆心,
又∵直线x-2y-2=0和直线2x+y+1=0互相垂直,
∴扇形的圆心角为90°,扇形的面积是圆的面积的四分之一,
∴圆x2+y2=4在区域D内的面积为π.
故答案为:π.
点评:本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.借助于平面区域特性,用几何方法处理代数问题,体现了数形结合思想、化归思想.
分析:先依据不等式组组
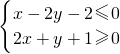 结合二元一次不等式(组)与平面区域的关系画出其表示的平面区域,再利用圆的方程画出图形,最后利用扇形面积公式计算即可.
结合二元一次不等式(组)与平面区域的关系画出其表示的平面区域,再利用圆的方程画出图形,最后利用扇形面积公式计算即可.解答:
 解:如图阴影部分表示
解:如图阴影部分表示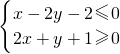 确定的平面区域,所以阴影部分扇形即为所求.
确定的平面区域,所以阴影部分扇形即为所求.由于
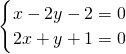 得两直线的交点(0,-1)即为圆心,
得两直线的交点(0,-1)即为圆心,又∵直线x-2y-2=0和直线2x+y+1=0互相垂直,
∴扇形的圆心角为90°,扇形的面积是圆的面积的四分之一,
∴圆x2+y2=4在区域D内的面积为π.
故答案为:π.
点评:本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.借助于平面区域特性,用几何方法处理代数问题,体现了数形结合思想、化归思想.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 所确定的平面区域的面积为0,则实数a的取值范围为
。
所确定的平面区域的面积为0,则实数a的取值范围为
。 所确定的平面区域,则圆
所确定的平面区域,则圆 在区域D内的弧长为
.
在区域D内的弧长为
. 所确定的平面区域记为
所确定的平面区域记为 ,则
,则 的最大值为
的最大值为