题目内容
如图为函数y=Asin(ωx+φ)+c(A>0,ω>0,φ>0)图象的一部分.
(1)求此函数的周期及最大值和最小值;
(2)求与这个函数图象关于直线x=2对称的函数解析式.

(1)求此函数的周期及最大值和最小值;
(2)求与这个函数图象关于直线x=2对称的函数解析式.

(1)由图可知,从4~12的图象是函数y=Asin(ωx+φ)+c(A>0,ω>0,φ>0)的
个周期的图象,所以A=
(4+2)=3
c=
(4-2)=1,
故函数的最大值为4,最小值为-2(4分)
∵
=12-4=8
T=
∴ω=
π,y=3sin(
x+φ)+1
把x=12,y=4代入上式,得φ=
所以,函数的解析式为:y=3sin(
x+
)+1(8分)
(2)设所求函数的图象上任一点(x,y)关于直线x=2的对称点为(x',y'),
则x'=4-x,y'=y代入y=3sin(
x+
)+1中得y=3sin
x+1
∴与函数y=3sin(
x+
)+1的图象关于直线x=2对称的函数解析式为:y=3sin
x+1(14分)
| 3 |
| 4 |
| 1 |
| 2 |
c=
| 1 |
| 2 |
故函数的最大值为4,最小值为-2(4分)
∵
| 3T |
| 4 |
T=
| 32 |
| 3 |
∴ω=
| 3 |
| 16 |
| 3π |
| 16 |
把x=12,y=4代入上式,得φ=
| π |
| 4 |
所以,函数的解析式为:y=3sin(
| 3π |
| 16 |
| π |
| 4 |
(2)设所求函数的图象上任一点(x,y)关于直线x=2的对称点为(x',y'),
则x'=4-x,y'=y代入y=3sin(
| 3π |
| 16 |
| π |
| 4 |
| 3π |
| 16 |
∴与函数y=3sin(
| 3π |
| 16 |
| π |
| 4 |
| 3π |
| 16 |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目


 时,函数
时,函数 取得最大值,则
取得最大值,则 .
. ,则
,则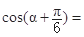 ____.
____.