题目内容
集合A={x||x|≤4,x∈R},B={x|(x+5)(x-a)≤0},则“AÍB”是“a>4”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
B
试题分析:因为A={x||x|≤4,x∈R}={x|
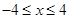 },若AÍB,
},若AÍB, 则B={x|(x+5)(x-a)≤0}={x|
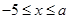 },所以须
},所以须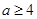 。反之,若a>4,则必有B={x|(x+5)(x-a)≤0}={x|
。反之,若a>4,则必有B={x|(x+5)(x-a)≤0}={x|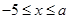 },AÍB,因此,“AÍB”是“a>4”的必要不充分条件,故选B。
},AÍB,因此,“AÍB”是“a>4”的必要不充分条件,故选B。点评:基础题,充要条件的判断问题,是高考不可少的内容,特别是充要条件可以和任何知识点相结合。充要条件的判断一般有三种思路:定义法、等价关系转化法、集合关系法。本题运用的是集合关系法。

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
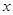 ,使
,使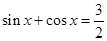 ;
;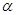 、
、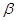 是第一象限角,且
是第一象限角,且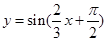 是偶函数;
是偶函数;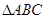 的三个内角,则
的三个内角,则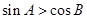
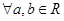 ,如果
,如果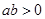 ,则
,则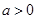 ”,则它的否命题是
”,则它的否命题是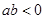 ,则
,则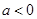
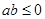 ,则
,则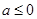
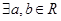 ,如果
,如果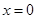 ,则
,则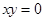 ”的逆命题
”的逆命题 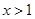 ,则
,则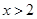 ”的逆否命题
”的逆否命题 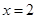 ,则
,则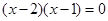 ”
”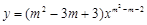 的图象不过原点,则m=1或m=2;
的图象不过原点,则m=1或m=2;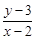 =
=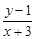 表示经过点A(2,3)、B(-3,1)的直线;
表示经过点A(2,3)、B(-3,1)的直线;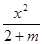 -
-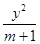 =1表示的曲线不可能是椭圆;
=1表示的曲线不可能是椭圆;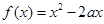 在
在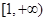 上是增函数,则
上是增函数,则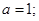 ②函数
②函数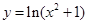 的值域是
的值域是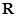 ;③函数
;③函数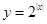 的最小值是1;④在同一坐标系中函数
的最小值是1;④在同一坐标系中函数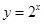 与
与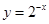 的图象关于
的图象关于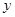 轴对称;其中正确命题的序号是 .
轴对称;其中正确命题的序号是 .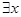 ∈R ,
∈R ,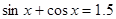
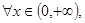
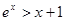
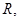

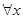 ∈
∈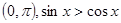
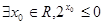
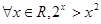
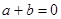 的充要条件是
的充要条件是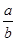 =-1
=-1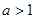 且
且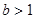 是
是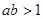 的充分条件
的充分条件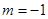 ”是“直线
”是“直线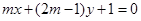 和直线
和直线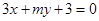 垂直”的
垂直”的