题目内容
若在数列 中,对任意正整数
中,对任意正整数 ,都有
,都有 (常数),则称数列
(常数),则称数列 为“等方和数列”,称
为“等方和数列”,称 为“公方和”,若数列
为“公方和”,若数列 为“等方和数列”,其前
为“等方和数列”,其前 项和为
项和为 ,且“公方和”为
,且“公方和”为 ,首项
,首项 ,则
,则 的最大值与最小值之和为( )
的最大值与最小值之和为( )
A、 B、
B、 C、
C、 D、
D、
【答案】
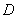
【解析】
试题分析:由 得
得 ,两等式相减得:
,两等式相减得: .又“公方和”为
.又“公方和”为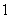 ,首项
,首项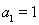 ,所以
,所以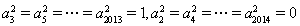 .所以
.所以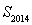 的最大值为1007,最小值为1005,其差为2.选D.
的最大值为1007,最小值为1005,其差为2.选D.
考点:1、新定义;2、数列.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目












 )(n∈N*)中,是否存在三个不同点Ak、Al、Am,使Ak、Al、Am在一条直线上?若存在,写出一组在一条直线上的三个点的坐标;若不存在,请说明理由.
)(n∈N*)中,是否存在三个不同点Ak、Al、Am,使Ak、Al、Am在一条直线上?若存在,写出一组在一条直线上的三个点的坐标;若不存在,请说明理由. )(n∈N*)中,是否存在三个不同点Ak、Al、Am,使Ak、Al、Am在一条直线上?若存在,写出一组在一条直线上的三个点的坐标;若不存在,请说明理由.
)(n∈N*)中,是否存在三个不同点Ak、Al、Am,使Ak、Al、Am在一条直线上?若存在,写出一组在一条直线上的三个点的坐标;若不存在,请说明理由.