��Ŀ����
��֪����F(x)=��1��������{an}��ͨ�ʽ��
��2��������{bn}�У�������������n��bn��![]() ����������SnΪ����{bn}��ǰn��ͣ��Ƚ�Sn��12�Ĵ�С��
����������SnΪ����{bn}��ǰn��ͣ��Ƚ�Sn��12�Ĵ�С��
��3���ڵ���An(2n, )(n��N*)�У��Ƿ����������ͬ��Ak��Al��Am��ʹAk��Al��Am��һ��ֱ���ϣ������ڣ�д��һ����һ��ֱ���ϵ�����������ꣻ�������ڣ���˵������.
)(n��N*)�У��Ƿ����������ͬ��Ak��Al��Am��ʹAk��Al��Am��һ��ֱ���ϣ������ڣ�д��һ����һ��ֱ���ϵ�����������ꣻ�������ڣ���˵������.
��1���⣺��![]() =f(an)����
=f(an)����![]() =
= =
= .?
.?
��![]() -
-![]() =4,��{
=4,��{![]() }����
}����![]() =1Ϊ���4Ϊ����ĵȲ�����.?
=1Ϊ���4Ϊ����ĵȲ�����.?
��![]() =1+��n-1����4=4n-3��?
=1+��n-1����4=4n-3��?
��an��0,��an=![]() . ?
. ?
��2���⣺��bn��![]() ,?
,?
��bn����(3n-1)+![]() ��=bn(4n2-1)=1.?
��=bn(4n2-1)=1.?
��bn=![]() =
=![]() (
(![]() -
-![]() ).?
).?
��Sn=b1+b2+��+bn?
=![]() ��(1-
��(1-![]() )+(
)+(![]() -
-![]() )+��+(
)+��+(![]() -
-![]() )��?
)��?
=![]() (1-
(1-![]() )��
)��![]() .?
.?
��Sn��![]() . ?
. ?
��3���⣺����An(2n,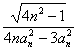 (n��N*)�в������й��ߵ�������. ?
(n��N*)�в������й��ߵ�������. ?
���ݣ�1�����ɵ�An(2n,![]() )(n��N*)��?
)(n��N*)��?
��x=2n,y=![]() ,��y=
,��y=![]() ��x��2��.?
��x��2��.?
�㣨x,y��������x2-y2=1(x��2,y��![]() )�ϣ�?
)�ϣ�?
����An(2n,![]() )������x2-y2=1(x��2,y��
)������x2-y2=1(x��2,y��![]() )�ϣ���ֱ�߷�����x2-y2=1������ɵķ�������������鲻ͬ�Ľ�.����ֱ����x2-y2=1�������������.?
)�ϣ���ֱ�߷�����x2-y2=1������ɵķ�������������鲻ͬ�Ľ�.����ֱ����x2-y2=1�������������.?
���Ե���An(2n,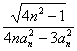 )(n��N*)�в������й��ߵ�������.
)(n��N*)�в������й��ߵ�������.

 ��֪����f(x)=
��֪����f(x)=
|
A��(
| ||||
B����
| ||||
C����
| ||||
D��[
|