题目内容
【题目】已知椭圆![]()
![]() 的左焦点
的左焦点![]() 左顶点
左顶点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知![]() ,
,![]() 是椭圆上的两点,
是椭圆上的两点,![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点.若
两侧的动点.若![]() ,试问直线
,试问直线![]() 的斜率是否为定值?请说明理由.
的斜率是否为定值?请说明理由.
【答案】(Ⅰ)![]() .(Ⅱ)
.(Ⅱ)![]() .
.
【解析】分析:(Ⅰ)根据条件依次求得![]() ,
,![]() 和
和![]() ,从而可得方程;
,从而可得方程;
(Ⅱ)当∠APQ=∠BPQ,则PA、PB的斜率之和为0,设直线PA的斜率为k,则PB的斜率为-k,PA的直线方程为y-3=k(x-2),PB的直线方程为y-9=-k(x-2),由此利用韦达定理结合已知条件能求出AB的斜率为定值![]() .
.
详解:(Ⅰ)由题意可得,![]() ,
,![]() 由
由![]() ,得
,得![]()
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)当![]() 时,
时,![]() ,
,![]() 的斜率之和为
的斜率之和为![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]() ,设
,设![]()
![]() ,
,![]() 的方程为
的方程为![]() .
.
联立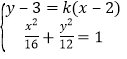 消
消![]() 得
得
![]() .
.
所以![]()
同理![]()
所以![]() ,
,![]() .
.
所以![]() .
.
所以![]() 的斜率为定值
的斜率为定值![]()

练习册系列答案
相关题目
【题目】![]() 市某机构为了调查该市市民对我国申办2034年足球世界杯的态度,随机选取了
市某机构为了调查该市市民对我国申办2034年足球世界杯的态度,随机选取了![]() 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:
不支持 | 支持 | 合计 | |
男性市民 |
| ||
女性市民 |
| ||
合计 |
|
|
(1)根据已知数据把表格数据填写完整;
(2)利用(1)完成的表格数据回答下列问题:
(i)能否有![]() 的把握认为支持申办足球世界杯与性别有关;
的把握认为支持申办足球世界杯与性别有关;
(ii)已知在被调查的支持申办足球世界杯的男性市民中有![]() 位退休老人,其中
位退休老人,其中![]() 位是教师,现从这
位是教师,现从这![]() 位退体老人中随机抽取
位退体老人中随机抽取![]() 人,求至多有
人,求至多有![]() 位老师的概率.
位老师的概率.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|


