题目内容
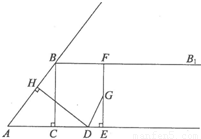 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值;
(3)以DH所在直线为对称轴,线段AC经轴对称变换后的图形为A′C′.
①当t>
 时,连接C′C,设四边形ACC′A′的面积为S,求S关于t的函数关系式;
时,连接C′C,设四边形ACC′A′的面积为S,求S关于t的函数关系式;②当线段A′C′与射线BB,有公共点时,求t的取值范围(写出答案即可).
【答案】分析:(1)先求出AB,再根据AD=AB以及AD=5t,CE=3t即可求出此时DE的长度;
(2)先根据t的取值不同对应的DE长不同,分两种情况分别讨论,再根据△DEG与△ACB相似时对应的边长之间的关系即可求出t的值;
(3)①先根据条件得到四边形ACC′A′是梯形;再根据三角形相似以及同一个角的正弦值相等分别求出梯形的上下底以及腰长即可求出S关于t的函数关系式;
②先求出A′在BB′上以及C′在BB′上时对应的t值,即可得到线段A′C′与射线BB′有公共点时,对应t的取值范围.
解答:解(1)∵∠ACB=90°,AC=3,BC=4,
∴AB=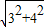 =5.
=5.
∵AD=5t,CE=3t,
∴当AD=AB时,5t=5,∴t=1.
∴AE=AC+CE=3+3t=6,∴DE=6-5=1.
(2)∵EF=BC=4,G是EF的中点∴GE=2.
当AD<AE(即t< )时,DE=AE-AD=3+3t-5t=3-2t,
)时,DE=AE-AD=3+3t-5t=3-2t,
若△DEG∽△ACB,则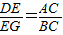 ,
,
若△DEG∽△BCA,则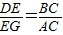 .
.
即有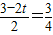 或
或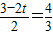 成立,
成立,
∴t= 或t=
或t= .
.
当AD>AE.(即t> )时,DE=AD-AE=5t-(3+3t)=2t-3.,
)时,DE=AD-AE=5t-(3+3t)=2t-3.,
若△DEG与△ACB相似,则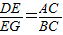 或
或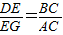 .
.
∴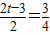 或
或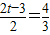 .
.
所以t= 或t=
或t=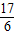 .
.
综上得,当t= 或
或 或
或 或
或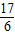 时.△DEG∽△ACB.
时.△DEG∽△ACB.
(3)①由轴对称变换得:AA′⊥DH,CC′⊥DH,
∴AA′∥CC′.易知OC≠AH故AA′≠CC′,
所以四边形ACC′A′是梯形.
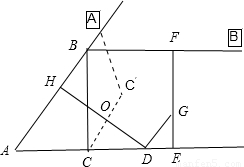
∵∠A=∠A,∠AHD=∠ACB=90°.
∴△AHD∽△ACB.∴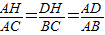 .
.
∴AH=3t,DH=4t
.∵sin∠ADH=sin∠CDO
∴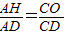 ,即
,即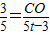
∴CO=3t- .
.
∴AA′=2AH=6t,CC′=2CO=6t-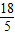 .
.
∵OD=CD•cos∠CD0=(5t-3)× =4t-
=4t-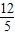 .
.
∴OH=DH-OD=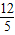 .
.
∴S= (AA′+CC′)•OH=
(AA′+CC′)•OH= (6t+6t-
(6t+6t-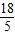 )×
)×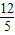 =
=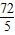 t-
t-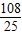 .
.
②当A′在BB′上时,A′和点B重合时,AH= AB=
AB= .此时cos∠BAC=
.此时cos∠BAC=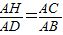 ,得AD=
,得AD= =
=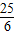 =5t,∴t=
=5t,∴t= ;
;
当C′在BB′上时,此时CC′=AB=5,∴CC′=6t+6t- =5,t=
=5,t=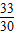 =
=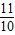 .
.
故当线段A′C′与射线BB′有公共点时所求t∈[ ,
,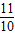 ].
].
点评:本题主要考查分类讨论思想以及相似三角形的应用问题.解决第二问的关键在于先根据t的取值不同对应的DE长不同,分两种情况分别讨论,避免出现漏解的情况.
(2)先根据t的取值不同对应的DE长不同,分两种情况分别讨论,再根据△DEG与△ACB相似时对应的边长之间的关系即可求出t的值;
(3)①先根据条件得到四边形ACC′A′是梯形;再根据三角形相似以及同一个角的正弦值相等分别求出梯形的上下底以及腰长即可求出S关于t的函数关系式;
②先求出A′在BB′上以及C′在BB′上时对应的t值,即可得到线段A′C′与射线BB′有公共点时,对应t的取值范围.
解答:解(1)∵∠ACB=90°,AC=3,BC=4,
∴AB=
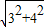 =5.
=5.∵AD=5t,CE=3t,
∴当AD=AB时,5t=5,∴t=1.
∴AE=AC+CE=3+3t=6,∴DE=6-5=1.
(2)∵EF=BC=4,G是EF的中点∴GE=2.
当AD<AE(即t<
 )时,DE=AE-AD=3+3t-5t=3-2t,
)时,DE=AE-AD=3+3t-5t=3-2t,若△DEG∽△ACB,则
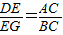 ,
,若△DEG∽△BCA,则
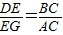 .
.即有
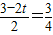 或
或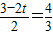 成立,
成立,∴t=
 或t=
或t= .
.当AD>AE.(即t>
 )时,DE=AD-AE=5t-(3+3t)=2t-3.,
)时,DE=AD-AE=5t-(3+3t)=2t-3.,若△DEG与△ACB相似,则
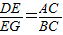 或
或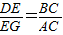 .
.∴
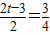 或
或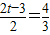 .
.所以t=
 或t=
或t=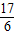 .
.综上得,当t=
 或
或 或
或 或
或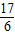 时.△DEG∽△ACB.
时.△DEG∽△ACB.(3)①由轴对称变换得:AA′⊥DH,CC′⊥DH,
∴AA′∥CC′.易知OC≠AH故AA′≠CC′,
所以四边形ACC′A′是梯形.

∵∠A=∠A,∠AHD=∠ACB=90°.
∴△AHD∽△ACB.∴
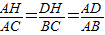 .
.∴AH=3t,DH=4t
.∵sin∠ADH=sin∠CDO
∴
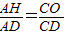 ,即
,即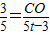
∴CO=3t-
 .
.∴AA′=2AH=6t,CC′=2CO=6t-
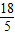 .
.∵OD=CD•cos∠CD0=(5t-3)×
 =4t-
=4t-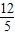 .
.∴OH=DH-OD=
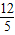 .
.∴S=
 (AA′+CC′)•OH=
(AA′+CC′)•OH= (6t+6t-
(6t+6t-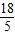 )×
)×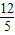 =
=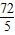 t-
t-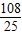 .
.②当A′在BB′上时,A′和点B重合时,AH=
 AB=
AB= .此时cos∠BAC=
.此时cos∠BAC=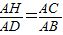 ,得AD=
,得AD= =
=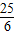 =5t,∴t=
=5t,∴t= ;
;当C′在BB′上时,此时CC′=AB=5,∴CC′=6t+6t-
 =5,t=
=5,t=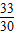 =
=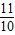 .
.故当线段A′C′与射线BB′有公共点时所求t∈[
 ,
,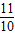 ].
].点评:本题主要考查分类讨论思想以及相似三角形的应用问题.解决第二问的关键在于先根据t的取值不同对应的DE长不同,分两种情况分别讨论,避免出现漏解的情况.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2
如图,在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2| 3 |
A、2
| ||||
| B、3 | ||||
C、
| ||||
D、
|
 如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )
如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )A、(0,
| ||||
B、(
| ||||
C、(
| ||||
| D、(2,4] |
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E. 如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P.
如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P. 8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=
8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=