题目内容
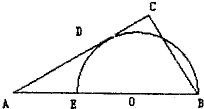 如图,已知EB是半圆O的直径,A是BE延长线上一点,AC切半圆O于点D,BC⊥AC于C,若BC=6,AC=8,则AE=
如图,已知EB是半圆O的直径,A是BE延长线上一点,AC切半圆O于点D,BC⊥AC于C,若BC=6,AC=8,则AE=分析:由已知中EB是半圆O的直径,A是BE延长线上一点,AC切半圆O于点D,BC⊥AC于C,连接OD,由切线的性质可得,OD⊥AC,则△AOD∽△ABC,再根据BC=6,AC=8,结合相似三角形对应边成比例,即可求出半径的长,进而得到AE,AD的长.
解答:解:连接OD,
∵AC切半圆O于点D,
∴OD⊥AC,
又∵BC⊥AC于C,
∴OD∥BC,
则△AOD∽△ABC
则
=
=
∵BC=6,AC=8,
∴AB=10
则OD=OE=OB=
∴AE=
,AD=5
故答案为:
,5
∵AC切半圆O于点D,
∴OD⊥AC,
又∵BC⊥AC于C,
∴OD∥BC,
则△AOD∽△ABC
则
| OD |
| BC |
| AO |
| AB |
| AD |
| AC |
∵BC=6,AC=8,
∴AB=10
则OD=OE=OB=
| 15 |
| 4 |
∴AE=
| 5 |
| 2 |
故答案为:
| 5 |
| 2 |
点评:本题考查的知识点是与圆有关的比例线段,其中根据切线的性质及相似三角形的判定定理得到△AOD∽△ABC是解答本题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
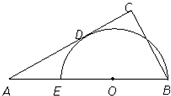 (几何证明选讲)如图,已知EB是半圆O的直径,A是BE延长线上一点,AC是半圆O的切线BC⊥AC于C,若BC=6,AC=8,则AE=
(几何证明选讲)如图,已知EB是半圆O的直径,A是BE延长线上一点,AC是半圆O的切线BC⊥AC于C,若BC=6,AC=8,则AE= (2008•深圳二模)(几何证明选讲选做题)如图,已知EB是半圆O的直径,A是BE延长线上一点,AC切半圆O于点D,BC⊥AC于C,DF⊥EB于点F,若BC=6,AC=8,则DF=
(2008•深圳二模)(几何证明选讲选做题)如图,已知EB是半圆O的直径,A是BE延长线上一点,AC切半圆O于点D,BC⊥AC于C,DF⊥EB于点F,若BC=6,AC=8,则DF= 如图,已知EB是半圆O的直径,A是BE延长线上一点,AC切半圆O于点D,BC⊥AC于点C,DF⊥EB于点F,若BC=6,AC=8,求DF的长.
如图,已知EB是半圆O的直径,A是BE延长线上一点,AC切半圆O于点D,BC⊥AC于点C,DF⊥EB于点F,若BC=6,AC=8,求DF的长.