题目内容
已知直线l1的参数方程为
(t是参数),直线l2的极坐标方程为ρ(2sinθ+cosθ)+6=0
(1)求直线l1与直线l2的交点P的坐标
(2)若直线l过点P,且与圆C:
(θ为参数)相交于A、B两点,|AB|=8,求直线l的方程.
|
(1)求直线l1与直线l2的交点P的坐标
(2)若直线l过点P,且与圆C:
|
分析:(1)把极坐标方程以及参数方程转化为直角坐标方程,通过求解方程即可得到l1与l2的交点A的直角坐标;
(2)由题意可得圆的方程x2+y2=25,若设直线l的参数方程为
(t为参数),代入圆的方程化简可得|AB|=|t1-t2|=
=8,解出方程即可得到直线的斜率进而得到直线l的方程.
(2)由题意可得圆的方程x2+y2=25,若设直线l的参数方程为
|
| 9(2cosα+sinα)2+55 |
解答:解:(1)∵直线l2的极坐标方程为ρ(2sinθ+cosθ)+6=0
∴直线l2的普通方程为2y+x+6=0
又∵直线l1的参数方程为
∴(-3+
t)+(-3+
t)+6=0
∴t=0,∴
∴P(-3,-
)
(2)由圆C的参数方程
⇒x2+y2=25,
设直线l的参数方程为①
(t为参数),①代入圆的方程x2+y2=25
得4t2-12(2cosα+sinα)t-55=0,
∴△=16[9(2cosα+sinα)2+55]>0,
所以方程有两相异实数根t1、t2,
∴|AB|=|t1-t2|=
=8,
化简有3cos2α+4sinαcosα=0,解之cosα=0或tanα=-
,
从而求出直线l的方程为x+3=0或3x+4y+15=0.
∴直线l2的普通方程为2y+x+6=0
又∵直线l1的参数方程为
|
∴(-3+
| 2 |
| ||
| 2 |
∴t=0,∴
|
∴P(-3,-
| 3 |
| 2 |
(2)由圆C的参数方程
|
设直线l的参数方程为①
|
得4t2-12(2cosα+sinα)t-55=0,
∴△=16[9(2cosα+sinα)2+55]>0,
所以方程有两相异实数根t1、t2,
∴|AB|=|t1-t2|=
| 9(2cosα+sinα)2+55 |
化简有3cos2α+4sinαcosα=0,解之cosα=0或tanα=-
| 3 |
| 4 |
从而求出直线l的方程为x+3=0或3x+4y+15=0.
点评:本题考查直线和圆的参数方程,参数方程与普通方程之间的转化,以及直线参数方程中参数的几何意义,求出|AB|,是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知直线l的参数方程为
(t为参数),则直线l的倾斜角为( )
|
| A、30° | B、60° |
| C、120° | D、150° |
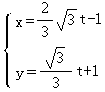 (t为参数)
l
(t为参数)
l