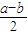题目内容
定义区间(c,d],[c,d),(c,d),[c,d]的长度均为d-c,其中d>c.则满足不等式
+
≥1, (a1>0, a2>0)的x构成的区间长度之和为
| 1 |
| a1x-1 |
| 1 |
| a2x-1 |
2
2
.分析:不妨令a1=a2=1,代入原式计算即可求得不等式中的x构成的区间长度之和.
解答:解:依题意,令a1=a2=1,代入原式得:
+
≥1,
即
-1=
≥0,
∴1<x≤3.
∴不等式中的x构成的区间长度之和为:3-1=2.
故答案为:2.
| 1 |
| x-1 |
| 1 |
| x-1 |
即
| 2 |
| x-1 |
| 3-x |
| x-1 |
∴1<x≤3.
∴不等式中的x构成的区间长度之和为:3-1=2.
故答案为:2.
点评:本题考查分式不等式的解法,特值法是捷径,也是解选择、填空题常用的方法,是降低难度,迅速求解的关键,属于难题.

练习册系列答案
相关题目
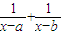 ≥1的x构成的区间的长度之和为 .
≥1的x构成的区间的长度之和为 .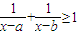 的x构成的区间的长度之和为( )
的x构成的区间的长度之和为( )