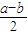题目内容
定义区间(c,d],(c,d],(c,d),[c,d]的长度均为d-c,其中d>c.若a,b是实数,且a>b,则满足不等式| 1 |
| x-a |
| 1 |
| x-b |
分析:不等式即
≤ 0,设 x2-(2+a+b)x+ab+a+b=0 的根为 x1和x2,则由求根公式可得这两个根的值,结合数轴,用穿根法来解的不等式的解集,从而求得解集构成的区间的长度之和.
| x2-(2+a+b)x+ab+a+b |
| (x-a)(x-b) |
解答: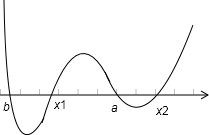 解:∵
解:∵
+
≥1,实数a>b,∴
≥1,即
≤ 0,
设x2-(2+a+b)x+ab+a+b=0的根为 x1和x2,则由求根公式可得,
x1=
,x2=
,把不等式的根排在数轴上,
穿根得不等式的解集为(b,x1)∪(a,x2 ),故解集构成的区间的长度之和为 (x1-b)+(x2-a )
=(x1+x2 )-a-b=(a+b+2)-a-b=2,
故选 D.
 解:∵
解:∵| 1 |
| x-a |
| 1 |
| x-b |
| 2x-(a+b) |
| (x-a)(x-b) |
| x2-(2+a+b)x+ab+a+b |
| (x-a)(x-b) |
设x2-(2+a+b)x+ab+a+b=0的根为 x1和x2,则由求根公式可得,
x1=
(a+b+2) -
| ||
| 2 |
(a+b+2) +
| ||
| 2 |
穿根得不等式的解集为(b,x1)∪(a,x2 ),故解集构成的区间的长度之和为 (x1-b)+(x2-a )
=(x1+x2 )-a-b=(a+b+2)-a-b=2,
故选 D.
点评:本题考查其他不等式的解法,解题的关键是掌握用穿根法解分式不等式和高次不等式的技巧,本题中令分子为0,得出x1和x2与系数的关键对解本题尤其关键.本题考查数形结合的思想,是不等式求解中难度较大的题型

练习册系列答案
相关题目
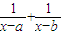 ≥1的x构成的区间的长度之和为 .
≥1的x构成的区间的长度之和为 .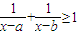 的x构成的区间的长度之和为( )
的x构成的区间的长度之和为( )