题目内容
7.已知O是正三角形△ABC内部的一点,$\overrightarrow{OA}$+2$\overrightarrow{OB}$+3$\overrightarrow{OC}$=$\overrightarrow{0}$,则△OAC的面积与△OAB的面积之比是( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | 1 |
分析 对所给的向量等式进行变形,根据变化后的条件对两个三角形的面积进行探究即可,
解答 解:$\overrightarrow{OA}$+2$\overrightarrow{OB}$+3$\overrightarrow{OC}$=$\overrightarrow{0}$,变为$\overrightarrow{OA}+\overrightarrow{OC}+2\overrightarrow{OB}+2\overrightarrow{OC}=\overrightarrow{0}$,
设D,E分别是对应边的中点,
由平行四边形法则知$\overrightarrow{OA}+\overrightarrow{OC}=2\overrightarrow{OE}$,2$\overrightarrow{OB}+2\overrightarrow{OC}=4\overrightarrow{OD}$,
故$\overrightarrow{OE}=-2\overrightarrow{OD}$,
由于正三角形ABC,
故S△AOC=$\frac{2}{3}$S△ADC=$\frac{2}{3}$×$\frac{1}{2}$×S△ABC=$\frac{1}{3}$S△ABC,
又D,E是中点,故O到AB的距离是正三角形ABC高的一半,
所以S△AOB=$\frac{1}{2}$×S△ABC
∴△OAC的面积与△OAB的面积之比为$\frac{2}{3}$.
故选:B
点评 本题考查向量的加法与减法,及向量共线的几何意义,本题中把两个三角形的面积都用三角形ABC的面积表示出来,这是求比值问题时常采用的思路,统一标准,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
15.以坐标轴为对称轴,以原点为顶点且过圆(x-1)2+(y+3)2=1的圆心的抛物线的方程是( )
| A. | y=3x2或y=-3x2 | B. | y=3x2 | C. | y2=-9x或y=3x2 | D. | y=-3x2或y2=9x |
18.已知函数f(x)=|x-a|-|x-4a|(a>0),若对?x∈R,都有f(2x)-1≤f(x),则实数a的最大值为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
15.${({{x^2}-\frac{1}{x}})^n}$展开式的二项式系数和为64,则其常数项为( )
| A. | -20 | B. | -15 | C. | 15 | D. | 20 |
16.若复数z满足z+2=(z-2)•i,则复数z的共轭复数$\overline{z}$=( )
| A. | -2i | B. | 2i | C. | 2+I | D. | 2-i |
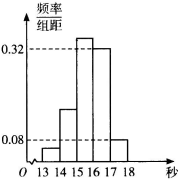 为了了解某学段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如右图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.
为了了解某学段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如右图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.