题目内容
选修4-4:坐标系统与参数方程:
在平面直角坐标系xOy中,求过椭圆
(φ为参数)的右焦点且与直线
(t为参数)平行的直线的普通方程.
在平面直角坐标系xOy中,求过椭圆
|
|
分析:将参数方程化为普通方程,求得椭圆的右焦点坐标,直线的斜率,从而可求得结论
解答:解:将椭圆
(φ为参数),消去参数可得
+
=1
∴椭圆
(φ为参数)的右焦点为(4,0)
直线
(t为参数),消去参数可得x-2y+2=0,直线的斜率为
过(4,0)与x-2y+2=0平行的直线为y-0=
(x-4),即x-2y-4=0
∴过椭圆
(φ为参数)的右焦点且与直线
(t为参数)平行的直线的普通方程为x-2y-4=0.
|
| x2 |
| 25 |
| y2 |
| 9 |
∴椭圆
|
直线
|
| 1 |
| 2 |
过(4,0)与x-2y+2=0平行的直线为y-0=
| 1 |
| 2 |
∴过椭圆
|
|
点评:本题以参数方程为载体,考查参数方程与普通方程的互化,考查直线的普通方程,属于基础题.

练习册系列答案
相关题目
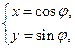 (
(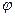 为参数)曲线C2的参数方程为
为参数)曲线C2的参数方程为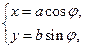 (
(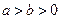 ,
,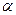 与C1,C2各有一个交点.当
与C1,C2各有一个交点.当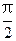 时,这两个交点重合.
时,这两个交点重合.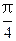 时,l与C1,C2的交点分别为A1,B1,当
时,l与C1,C2的交点分别为A1,B1,当 (
(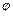 为参数),曲线C2的参数方程为
为参数),曲线C2的参数方程为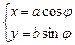 (
(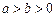 ,
,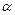 与C1,C2各有一个交点.当
与C1,C2各有一个交点.当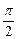 时,这两个交点重合.
时,这两个交点重合.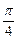 时,l与C1,C2的交点分别为A1,B1,当
时,l与C1,C2的交点分别为A1,B1,当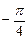 时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.
时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积. (
( 为参数)曲线C2的参数方程为
为参数)曲线C2的参数方程为 (
( ,
, 与C1,C2各有一个交点.当
与C1,C2各有一个交点.当 时,这两个交点重合。
时,这两个交点重合。 时,l与C1,C2的交点分别为A1,B1,当
时,l与C1,C2的交点分别为A1,B1,当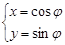 (
(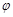 为参数),曲线C2的参数方程为
为参数),曲线C2的参数方程为 (
(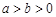 ,
,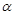 与C1,C2各有一个交点.当
与C1,C2各有一个交点.当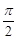 时,这两个交点重合.
时,这两个交点重合. 时,l与C1,C2的交点分别为A1,B1,当
时,l与C1,C2的交点分别为A1,B1,当 时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.
时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.