题目内容
(23)(本小题满分10分)选修4-4:坐标系统与参数方程
在平面直角坐标系xOy中,曲线C1的参数方程为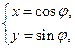 (
(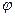 为参数)曲线C2的参数方程为
为参数)曲线C2的参数方程为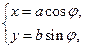 (
(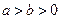 ,
,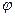 为参数)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=
为参数)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=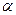 与C1,C2各有一个交点.当
与C1,C2各有一个交点.当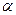 =0时,这两个交点间的距离为2,当
=0时,这两个交点间的距离为2,当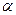 =
=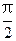 时,这两个交点重合.
时,这两个交点重合.
(I)分别说明C1,C2是什么曲线,并求出a与b的值;
(II)设当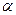 =
=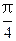 时,l与C1,C2的交点分别为A1,B1,当
时,l与C1,C2的交点分别为A1,B1,当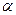 =-
=-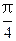 时,l与C1,
时,l与C1,
C2的交点为A2,B2,求四边形A1A2B2B1的面积.
解析:(I)C1为圆,C2为椭圆.
当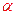 =0时,射线l与C1,C2交点的直角坐标分别是(1,0),(a,0),因为这两点间的距离为2,所以a=3.
=0时,射线l与C1,C2交点的直角坐标分别是(1,0),(a,0),因为这两点间的距离为2,所以a=3.
当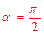 时,射线l与C1,C2交点的直角坐标分别是(0,1),(
时,射线l与C1,C2交点的直角坐标分别是(0,1),( 0,b),因为这两点重合,所以b=1.
0,b),因为这两点重合,所以b=1.
(II)C1,C2的普通方程分别为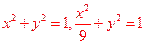 ,
,
当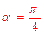 时,射线l与C1交点A1的横坐标是
时,射线l与C1交点A1的横坐标是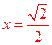 ,与C2交点B1的横坐标是
,与C2交点B1的横坐标是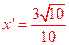 ;
;
当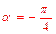 时,射线l与C1、C2的两个交点A2、B2的分别与A1、B1关于x轴对称,因此,四边形与A1 A2B2B1为梯形.
时,射线l与C1、C2的两个交点A2、B2的分别与A1、B1关于x轴对称,因此,四边形与A1 A2B2B1为梯形.
故四边形与A1 A2B2B1的面积为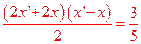 .
.
解析

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 (t为参数),C2
(t为参数),C2 (
( 为参数),
为参数), =
= 时,求C1与C2的交点坐标;
时,求C1与C2的交点坐标; (t为参数),C2
(t为参数),C2 (
( 为参数),
为参数), =
= 时,求C1与C2的交点坐标;
时,求C1与C2的交点坐标; 的值.
的值.
 ,点F1、F2为其左、右焦点,直线l的参数方程为
,点F1、F2为其左、右焦点,直线l的参数方程为
 恒成立,记实数M的最大值是m。
恒成立,记实数M的最大值是m。
 的值.
的值.
 ,点F1、F2为其左、右焦点,直线l的参数方程为
,点F1、F2为其左、右焦点,直线l的参数方程为
 恒成立,记实数M的最大值是m。
恒成立,记实数M的最大值是m。