题目内容
【必做题】(本题满分10分)
如图所示的几何体是由以等边三角形![]() 为底面的棱柱被平面
为底面的棱柱被平面![]() 所截而得,已知
所截而得,已知![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 相交所成锐角二面角的余弦值;
相交所成锐角二面角的余弦值;
(Ⅲ)在![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]()
![]() 平面
平面![]() ?如果存在,求出
?如果存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.

【必做题】(本题满分10分)
如图所示的几何体是由以等边三角形![]() 为底面的棱柱被平面
为底面的棱柱被平面![]() 所截而得,已知
所截而得,已知![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 相交所成锐角二面角的余弦值;
相交所成锐角二面角的余弦值;
(Ⅲ)在![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]()
![]() 平面
平面![]() ?如果存在,求出
?如果存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.

提示:如图,以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
![]() ,
,![]() ,
,![]() ,
,![]() . ……2分
. ……2分
(Ⅰ)![]() ,
,![]() ,
,
所以![]() ,即
,即![]() . ……2分
. ……2分
(Ⅱ)平面![]() 的法向量为
的法向量为![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,![]() .
.
由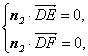 得
得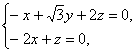 所以
所以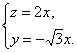
取![]() ,得
,得![]() .
.
所以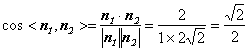 ,所以平面
,所以平面![]() 与平面
与平面![]() 相交所成锐角二面角的余弦值为
相交所成锐角二面角的余弦值为![]() . ……6分
. ……6分
(Ⅲ)假设在![]() 存在一点
存在一点![]() , 设
, 设![]() ,
,
因为![]() ,故
,故![]() ,
,
所以![]() ,所以
,所以![]() .
.
因为![]()
![]() 平面
平面![]() ,所以
,所以![]() 与平面
与平面![]() 的法向量
的法向量![]() 共线,
共线,
所以![]() ,解得
,解得![]() ,
,
所以![]() ,即
,即![]() ,所以
,所以![]() . ……10分
. ……10分
点评:该题考查空间向量的坐标表示、空间向量的数量积、空间向量的共线与垂直、直线的方向向量与平面的法向量;是中档题。

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
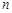 ,
,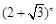 必可表示成
必可表示成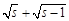 的形式,其中
的形式,其中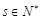 .
. ,从中任取一个.
,从中任取一个. ,至少存在另一个正整数
,至少存在另一个正整数 ,且
,且 ,使得
,使得 ”的概率;
”的概率; 为组成该数的相同数字的个数的最大值,求
为组成该数的相同数字的个数的最大值,求 ,则“海宝”卡至少多少张?
,则“海宝”卡至少多少张? 表示获奖的人数,求
表示获奖的人数,求