题目内容
4.已知实数x,y满足可行域D:$\left\{\begin{array}{l}{x+3y-3≥0}\\{x-y+1≥0}\\{3x+y-9≤0}\end{array}\right.$,曲线T:|x|+|y-5|+a=0,恰好平分可行域D的面积,则a的值为( )| A. | -4 | B. | -4$\sqrt{2}$ | C. | -6 | D. | 2$\sqrt{2}$-8 |
分析 作出不等式组对应的平面区域,确定x,y的取值范围将曲线进行化简,利用面积关系进行转化求即可即可.
解答 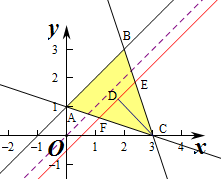 解:作出不等式组对应的平面区域如图:则A(0,1),C(3,0),
解:作出不等式组对应的平面区域如图:则A(0,1),C(3,0),
由$\left\{\begin{array}{l}{x-y+1=0}\\{3x+y-9=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$,即B(2,3),
则x≥0且0≤y≤3,
则曲线T:|x|+|y-5|+a=0,等价为x-y+5+a=0,
则曲线x-y+5+a=0与直线AB:x-y+1=0平行,
则C到AB:x-y+1=0的距离dAB=$\frac{|3-0+1|}{\sqrt{2}}=\frac{4}{\sqrt{2}}$=2$\sqrt{2}$,
|AB|=$\sqrt{{2}^{2}+{2}^{2}}=\sqrt{8}=2\sqrt{2}$,
则△ABC的面积S=$\frac{1}{2}×2\sqrt{2}×2\sqrt{2}$=4.
∵T:|x|+|y-5|+a=0,恰好平分可行域D的面积,
∴设C到x-y+5+a=0的距离d,
则$(\frac{d}{{d}_{AB}})^{2}=\frac{1}{2}$,即$\frac{d}{{d}_{AB}}=\sqrt{\frac{1}{2}}=\frac{\sqrt{2}}{2}$,
即d=$\frac{\sqrt{2}}{2}×{d}_{AB}$=$\frac{\sqrt{2}}{2}×2\sqrt{2}=2$,
则d=$\frac{|3-0+5+a|}{\sqrt{2}}=\frac{|8+a|}{\sqrt{2}}$=2,
即|a+8|=2$\sqrt{2}$,
解得a+8=2$\sqrt{2}$,或a+8=-2$\sqrt{2}$,
即a=2$\sqrt{2}$-8或a=-2$\sqrt{2}$-8(舍).
故选:D.
点评 本题主要考查线性规划的应用,根据图象将曲线进行化简是解决本题的关键,考查学生的运算和推理能力.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案| A. | y=-2x-3 | B. | y=x | C. | y=2x+1 | D. | y=-1 |
| A. | φ | B. | {d} | C. | {a,c} | D. | {b,e} |
 如图,四棱锥P-ABCD中,底面ABCD为矩形,PB=PC=AB,PB⊥平面PDC,E为棱PC的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PB=PC=AB,PB⊥平面PDC,E为棱PC的中点.