题目内容
某国由于可耕地面积少,计划从今年起的五年填湖围造一部分生产和生活用地,若填湖费、购置排水设备费等所需经费与当年所填湖造地面积x(亩)的平方成正比,其比例系数为a,设每亩水面的年平均经济效益为b元,填湖造地后的每亩土地的年平均收益为c元(其中a,b,c均为常数).(1)若按计划填湖造地,且使得今年的收益不小于支出,试求所填面积x的最大值.
(2)如果填湖造地面积按每年1%的速度减少,为保证水面的畜洪能力和环保要求,填湖造地的总面积不能超过现有水面面积的25%,求今年填湖造地的面积最多只能占现有水面的百分之几.
注:根据下列近似值进行计算:
0.992≈0.98,0.992≈0.97,0.994≈0.96,0.995≈0.95,0.996≈0.94,0.997≈0.93.
【答案】分析:(1)依题意收益不小于支出的条件可以表示为cx≥ax2+bx,化简的x[ax-(c-b)]≤0,故只需分别看c-b≤0和c-b>0两种情况下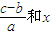 的关系.
的关系.
(2)设该地现在水面m亩,今年填湖造地x亩.依题意可得到关系式,进而求出x的范围.
解答:解:(1)收益不小于支出的条件可以表示为cx≥ax2+bx,
所以ax2+(b-c)x≤0,x[ax-(c-b)]≤0.
当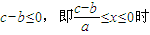 ,此时不能填湖造地,
,此时不能填湖造地,
当c-b>0,即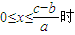 ,此时所填面积的最大值为
,此时所填面积的最大值为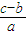 亩;
亩;
(2)设该地现在水面m亩,今年填湖造地x亩.
则x+(1-1%)x+(1-1%)2x+(1-1%)3x+(1-1%)4x≤0.25m,
即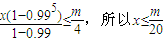 ,
,
因此今年填湖造地面积最多只能占现有水面的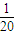 .
.
点评:本题主要考查了等比数列的求和问题.数列的求和问题是数列重要内容之一常与函数、不等式、极限等一块考查,平时应多积累求和的各种方法.
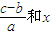 的关系.
的关系.(2)设该地现在水面m亩,今年填湖造地x亩.依题意可得到关系式,进而求出x的范围.
解答:解:(1)收益不小于支出的条件可以表示为cx≥ax2+bx,
所以ax2+(b-c)x≤0,x[ax-(c-b)]≤0.
当
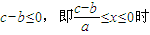 ,此时不能填湖造地,
,此时不能填湖造地,当c-b>0,即
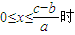 ,此时所填面积的最大值为
,此时所填面积的最大值为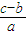 亩;
亩;(2)设该地现在水面m亩,今年填湖造地x亩.
则x+(1-1%)x+(1-1%)2x+(1-1%)3x+(1-1%)4x≤0.25m,
即
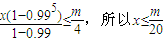 ,
,因此今年填湖造地面积最多只能占现有水面的
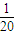 .
.点评:本题主要考查了等比数列的求和问题.数列的求和问题是数列重要内容之一常与函数、不等式、极限等一块考查,平时应多积累求和的各种方法.

练习册系列答案
相关题目