题目内容
4．求[2sin50°+sin10°（1+$\sqrt{3}$tan10°）]•$\sqrt{2si{n}^{2}80°}$的值．分析 首先利用关系式进行恒等变换，主要考察切化弦思想的应用，进一步通过三角的恒等变换求出结果．
解答 解：[2sin50°+sin10°（1+$\sqrt{3}$tan10°）]•$\sqrt{2si{n}^{2}80°}$
=[$2sin50°+sin10°（1+\sqrt{3}\frac{sin10°}{cos10°}）]$$•\sqrt{2{sin}^{2}80°}$
=[2sin50°+sin10°$\begin{array}{c}\\（\frac{cos10°+\sqrt{3}sin10°}{cos10°}）]\end{array}\right.$$•\sqrt{2{sin}^{2}80°}$
=[2sin50°+sin10°$\frac{2sin40°}{cos10°}$）$•\sqrt{2}cos10°$
=2$\sqrt{2}$（sin50°cos10°+cos50°sin10°）
=2$\sqrt{2}sin60°$
=$\sqrt{6}$．
点评 本题考查的知识要点：三角函数的关系式的恒等变换，特殊角的三角函数的值得应用，主要考查学生的恒等变换能力和应用能力．
练习册系列答案
阅读快车系列答案
相关题目
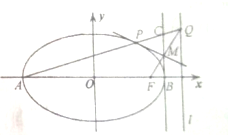如图，设A，B分比为椭圆E$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右顶点，P是椭圆E上不同于A，B的一动点，点F是椭圆E的右焦点，直线l是椭圆E的右准线，若直线AP与直线：x=a和l分别相较于C，Q两点，FQ与直线BC交于M．
某校团委会组织该校高中一年级某班以小组为单位利用周末时间进行了一次社会实践活动，且每个小组有5名同学，在实践活动结束后，学校团委会对该班的所有同学都进行了测评，该班的A、B两个小组所有同学所得分数（百分制）的茎叶图如图所示，其中B组一同学的分数已被污损，但知道B组学生的平均分比A组学生的平均分高1分．
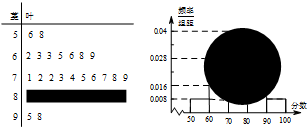
如图，在直三棱柱ABC-A1B1C1中，底面△ABC为等边三角形，AB=4，AA1=5，点M是BB1中点