题目内容
13. 如图,在直三棱柱ABC-A1B1C1中,底面△ABC为等边三角形,AB=4,AA1=5,点M是BB1中点
如图,在直三棱柱ABC-A1B1C1中,底面△ABC为等边三角形,AB=4,AA1=5,点M是BB1中点(Ⅰ)求证:平面A1MC⊥平面AA1C1C
(Ⅱ)求点A到平面A1MC的距离.
分析 (Ⅰ)连结ME,利用直三棱柱ABC-A1B1C1,结合已知,只要判断ME⊥平面AA1C1C,利用面面垂直的判定定理证明;
(Ⅱ)过点A作AH⊥A1C于点H,由(Ⅰ)知AH⊥平面AA1C1C,得到AH即为点A到平面A1MC的距离,利用直角三角形A1AC,可求
解答 (Ⅰ)证明:记AC1与A1C的交点为E.连结ME.
如图
∵直三棱柱ABC-A1B1C1,点M是BB1中点,
∴MA1=MA=MC1=MC=$\frac{\sqrt{89}}{2}$.
因为点E是AC1,A1C的中点,
所以ME⊥AC1且ME⊥A1C,…(4分)
从而ME⊥平面AA1C1C.
因为ME?平面A1MC,所以平面A1MC⊥平面AA1C1C.…(6分)
(Ⅱ)解:过点A作AH⊥A1C于点H,
如图,
由(Ⅰ)知平面A1MC⊥平面AA1C1C,平面A1MC∩平面AA1C1C=A1C,
而AH⊥平面AA1C1C
∴AH即为点A到平面A1MC的距离.…(9分)
在△A1AC中,∠A1AC=90°,
A1A=5,AC=4∴${A}_{1}C=\sqrt{41}$
∴AH=$\frac{5×4}{\sqrt{41}}=\frac{20\sqrt{41}}{41}$
即点A到平面A1MC的距离为$\frac{20\sqrt{41}}{41}$. …(12分)
点评 本题考查面面垂直的判定定理和性质定理的运用,体现了转化的思想.属于中档题.

练习册系列答案
相关题目
18.已知a=${log}_{2}\frac{1}{3}$,b=lg5,c=ln$\sqrt{e}$,则a、b、c的大小关系为( )
| A. | <b<a | B. | c<a<b | C. | a<c<b | D. | a<b<c |
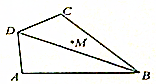 如图,在四边形ABCD中,∠BAD=90°,∠ADC=120°,AD=DC=2,AB=4,动点M在△BCD内(含边界)运动,设$\overrightarrow{AM}$=$λ\overrightarrow{AB}$+μ$\overrightarrow{AD}$,则λ+μ的取值范围是[1,$\frac{\sqrt{3}}{4}+\frac{3}{2}$].
如图,在四边形ABCD中,∠BAD=90°,∠ADC=120°,AD=DC=2,AB=4,动点M在△BCD内(含边界)运动,设$\overrightarrow{AM}$=$λ\overrightarrow{AB}$+μ$\overrightarrow{AD}$,则λ+μ的取值范围是[1,$\frac{\sqrt{3}}{4}+\frac{3}{2}$].