题目内容
用二分法求函数y=f(x)在区间[2,4]上零点的近似解,经验证有f(2)•f(4)<0.取区间的中点为x1=3,计算得f(2)•f(x1)<0,则此时零点x0∈
(2,3)
(2,3)
;(填区间)分析:方程的实根就是对应函数f(x)的零点,由f(2)•f(x1)<0知,f(x)零点所在的区间为(2,x1),进而得到答案
解答:解:由题意可知:对于函数y=f(x)在区间[2,4]上,
有f(2)•f(4)<0,
利用函数的零点存在性定理,所以函数在(2,4)上有零点.
取区间的中点x1=
=3,
∵f(2)•f(x1)<0,
∴利用函数的零点存在性定理,函数在(2,3)上有零点.
故答案为:(2,3).
有f(2)•f(4)<0,
利用函数的零点存在性定理,所以函数在(2,4)上有零点.
取区间的中点x1=
| 2+4 |
| 2 |
∵f(2)•f(x1)<0,
∴利用函数的零点存在性定理,函数在(2,3)上有零点.
故答案为:(2,3).
点评:本题考查用二分法求方程的根所在的区间的方法,方程的实根就是对应函数f(x)的零点,函数在区间上存在零点的条件是函数在区间的端点处的函数值异号.属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
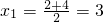 ,计算得f(2)•f(x1)<0,则此时零点x0∈________.(填区间)
,计算得f(2)•f(x1)<0,则此时零点x0∈________.(填区间)