题目内容
若关于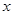 的不等式
的不等式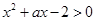 在区间
在区间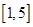 上有解,则实数
上有解,则实数 的取值范围为( )
的取值范围为( )
A. | B. | C.(1,+∞) | D.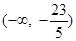 |
A
解析试题分析:根据题意,由于关于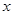 的不等式
的不等式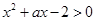 在区间
在区间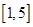 上有解,则可知
上有解,则可知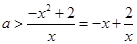 ,由于函数y=
,由于函数y=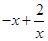 在定义域内是增函数,故可知有解的话只要a大于函数的最小值即可,即
在定义域内是增函数,故可知有解的话只要a大于函数的最小值即可,即 ,故可知a的范围是
,故可知a的范围是 ,故选A.
,故选A.
考点:不等式
点评:对于一元二次不等式的给定区间上有解问题,可以分离参数法得到,这是一种常用的转化角度,基础题。

练习册系列答案
相关题目
若集合 ,则实数a的取值范围是
,则实数a的取值范围是
A.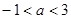 | B.1<a<4 | C.0<a<3 | D.0<a<4 |
二次不等式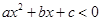 的解集是全体实数的条件是( )
的解集是全体实数的条件是( )
A.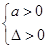 | B. | C.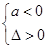 | D.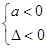 |
不等式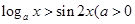 且
且 对任意
对任意 都成立,则
都成立,则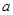 的取值
的取值
范围为
A.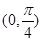 | B. | C.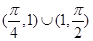 | D.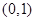 |
已知x>0,y>0,x+y+xy="2," 则x+y的最小值是
A.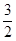 | B.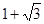 | C. | D. |
方程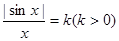 有且仅有两个不同的实数解
有且仅有两个不同的实数解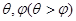 ,则以下结论正确的为( )
,则以下结论正确的为( )
A.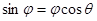 | B. |
C.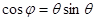 | D. |
若不等式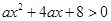 的解集为
的解集为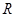 ,则实数
,则实数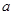 的取值范围是
的取值范围是
A.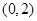 | B.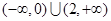 |
C.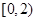 | D.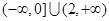 |
不等式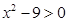 的解集为( )
的解集为( )
A.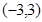 | B.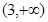 | C.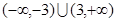 | D.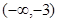 |
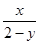 ,若关于x的不等式(x-a)⊙(x+1-a)>0的解集是集合{x|-2≤x≤2,x∈R}的子集,则实数a的取值范围是( )
,若关于x的不等式(x-a)⊙(x+1-a)>0的解集是集合{x|-2≤x≤2,x∈R}的子集,则实数a的取值范围是( )