题目内容
已知x>0,y>0,x+y+xy="2," 则x+y的最小值是
A.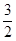 | B.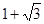 | C. | D. |
C
解析试题分析:根据题意,由于x>0,y>0,x+y+xy=2,根据已知的关系式,要求解x+y的最小值,要想到运用均值不等式,即有 ,则可知
,则可知 ,故可知答案为
,故可知答案为 ,选C.
,选C.
考点:均值不等式
点评:此题主要考查基本不等式的用法,对于不等式a+b≥2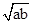 在求最大值最小值的问题中应用非常广泛,需要同学们多加注意
在求最大值最小值的问题中应用非常广泛,需要同学们多加注意

练习册系列答案
相关题目
不等式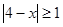 的解集为
的解集为
A. | B. | C. | D.R |
不等式 的解( )
的解( )
A.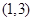 | B.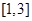 | C.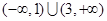 | D. |
若方程 在(0,1)内恰有一解,则a的取值范围是( )
在(0,1)内恰有一解,则a的取值范围是( )
A. | B.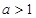 | C. | D. |
若关于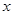 的不等式
的不等式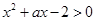 在区间
在区间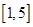 上有解,则实数
上有解,则实数 的取值范围为( )
的取值范围为( )
A. | B. | C.(1,+∞) | D.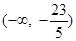 |
对一切实数x,不等式 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
A. | B. | C. | D.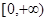 |
定义: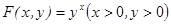 ,已知数列
,已知数列 满足
满足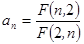
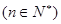 ,若对任意正整数
,若对任意正整数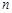 ,都有
,都有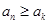
 成立,则
成立,则 的值为 ( )
的值为 ( )
| A.2 | B.1 | C.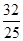 | D.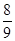 |
设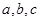 均为正数,且
均为正数,且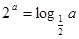 ,
,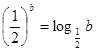 ,
,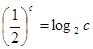 则( )
则( )
A. | B.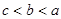 | C.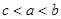 | D.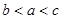 |
不等式-6x2-x+2≤0的解集是( )
A. | B. |
C. | D. |