题目内容
已知函数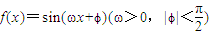
的导函数y=f′（x）的部分图象如图所示，且导函数f'（x）的最小值为-2，则函数的表达式为 ．
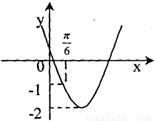-1
【答案】分析：求出函数的导函数，结合图象求出ω，利用图象经过
，点的坐标适合导函数方程，求出ϕ即可，确定函数的解析式．
解答：解：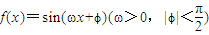
所以f′（x）=ωcos（ωx+ϕ），由图象可知：ω=2；
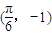在导函数的图象上，所以-1=2cos（2×
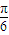+ϕ），∴ϕ=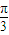
所以函数的解析式为：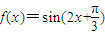
故答案为：
点评：本题是基础题，考查函数的导函数知识，三角函数图象求函数的解析式，注意两点：一是导函数的求法；二是y=Asin（ωx+φ）中参数的物理意义，考查分析问题解决问题的能力．
，点的坐标适合导函数方程，求出ϕ即可，确定函数的解析式．解答：解：
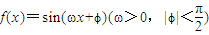所以f′（x）=ωcos（ωx+ϕ），由图象可知：ω=2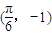；在导函数的图象上，所以-1=2cos（2×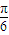+ϕ），∴ϕ=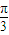所以函数的解析式为：
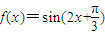
故答案为：
点评：本题是基础题，考查函数的导函数知识，三角函数图象求函数的解析式，注意两点：一是导函数的求法；二是y=Asin（ωx+φ）中参数的物理意义，考查分析问题解决问题的能力．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
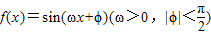的导函数y=f′（x）的部分图象如图所示，且导函数f'（x）的最小值为-2，则函数的表达式为 ．
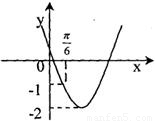-1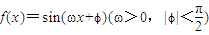
的导函数y=f'（x）的部分图象如图所示，且导函数f'（x）有最小值-2，则ω= ，ϕ= ．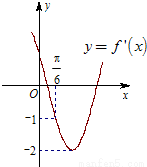
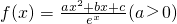的导函数y=f'（x）的两个零点为-3和0．
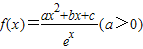的导函数y=f'（x）的两个零点为-3和0．