题目内容
已知函数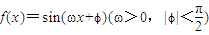
的导函数y=f'（x）的部分图象如图所示，且导函数f'（x）有最小值-2，则ω= ，ϕ= ．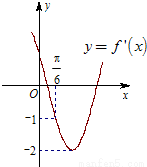
【答案】分析：求出f（x）=sin（ωx+φ）的导函数，可得f′（x）=ωcos（ωx+φ），根据其图象得出参数的值即可．
解答：解：由导函数的图象知，ω=2，又函数图象过点（
，-1），故有2cos（2×
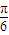+φ）=-1，解得2×
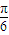+φ=2kπ+
或2kπ-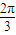
，k∈z，即φ=2kπ+
或φ=2kπ-πk∈z，
又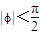
当k=0时，φ=
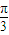符合题意
故答案为2，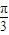
点评：本题考查由三角函数的部分图象得出其解析式，求解本题的关键一是正确求出导数，二是由图象及所给的条件得出ω，本题中求φ是难点也是易错点，做题时要注意总结求值的规律．
解答：解：由导函数的图象知，ω=2，又函数图象过点（
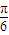，-1），故有2cos（2×+φ）=-1，解得2×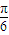+φ=2kπ+或2kπ-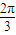，k∈z，即φ=2kπ+或φ=2kπ-πk∈z，又
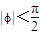当k=0时，φ=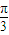符合题意故答案为2，
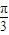
点评：本题考查由三角函数的部分图象得出其解析式，求解本题的关键一是正确求出导数，二是由图象及所给的条件得出ω，本题中求φ是难点也是易错点，做题时要注意总结求值的规律．
练习册系列答案
相关题目
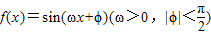的导函数y=f′（x）的部分图象如图所示，且导函数f'（x）的最小值为-2，则函数的表达式为 ．
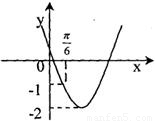-1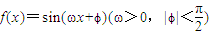
的导函数y=f′（x）的部分图象如图所示，且导函数f'（x）的最小值为-2，则函数的表达式为 ．
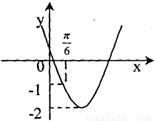-1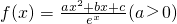
的导函数y=f'（x）的两个零点为-3和0．
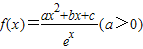的导函数y=f'（x）的两个零点为-3和0．