题目内容
已知函数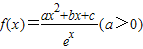 的导函数y=f'(x)的两个零点为-3和0.
的导函数y=f'(x)的两个零点为-3和0.(Ⅰ)求f(x)的单调区间;
(Ⅱ)若f(x)的极小值为-e3,求f(x)在区间[-5,+∞)上的最大值.
【答案】分析:(Ⅰ)求导数f′(x),根据y=f'(x)的两个零点-3和0以及a的符号,即可解得不等式f'(x)>0,f'(x)<0,从而得到函数f(x)的单调区间;
(Ⅱ)由(Ⅰ)及所给已知条件可求出f(x),再利用导数即可求得函数f(x)在闭区间上的最大值;
解答:解:(Ⅰ)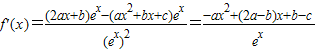 ,
,
令g(x)=-ax2+(2a-b)x+b-c,
因为ex>0,所以y=f'(x)的零点就是g(x)=-ax2+(2a-b)x+b-c的零点,且f'(x)与g(x)符号相同.
又因为a>0,所以-3<x<0时,g(x)>0,即f'(x)>0,
当x<-3,或x>0时,g(x)<0,即f'(x)<0,
所以f(x)的单调增区间是(-3,0),单调减区间是(-∞,-3),(0,+∞).
(Ⅱ)由(Ⅰ)知,x=-3是f(x)的极小值点,所以有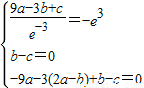 ,
,
解得a=1,b=5,c=5,
所以 .
.
∵f(x)的单调增区间是(-3,0),单调减区间是(-∞,-3),(0,+∞),
∴f(0)=5为函数f(x)的极大值,
∴f(x)在区间[-5,+∞)上的最大值取f(-5)和f(0)中的最大者.
而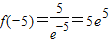 >5,所以函数f(x)在区间[-5,+∞)上的最大值是5e5.
>5,所以函数f(x)在区间[-5,+∞)上的最大值是5e5.
点评:本题考查利用导数研究函数的单调性及函数在闭区间上的最值问题,考查学生分析问题解决问题的能力,属中档题.
(Ⅱ)由(Ⅰ)及所给已知条件可求出f(x),再利用导数即可求得函数f(x)在闭区间上的最大值;
解答:解:(Ⅰ)
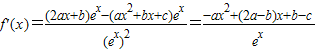 ,
,令g(x)=-ax2+(2a-b)x+b-c,
因为ex>0,所以y=f'(x)的零点就是g(x)=-ax2+(2a-b)x+b-c的零点,且f'(x)与g(x)符号相同.
又因为a>0,所以-3<x<0时,g(x)>0,即f'(x)>0,
当x<-3,或x>0时,g(x)<0,即f'(x)<0,
所以f(x)的单调增区间是(-3,0),单调减区间是(-∞,-3),(0,+∞).
(Ⅱ)由(Ⅰ)知,x=-3是f(x)的极小值点,所以有
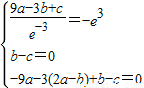 ,
,解得a=1,b=5,c=5,
所以
 .
.∵f(x)的单调增区间是(-3,0),单调减区间是(-∞,-3),(0,+∞),
∴f(0)=5为函数f(x)的极大值,
∴f(x)在区间[-5,+∞)上的最大值取f(-5)和f(0)中的最大者.
而
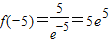 >5,所以函数f(x)在区间[-5,+∞)上的最大值是5e5.
>5,所以函数f(x)在区间[-5,+∞)上的最大值是5e5.点评:本题考查利用导数研究函数的单调性及函数在闭区间上的最值问题,考查学生分析问题解决问题的能力,属中档题.

练习册系列答案
相关题目
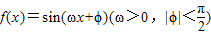 的导函数y=f′(x)的部分图象如图所示,且导函数f'(x)的最小值为-2,则函数的表达式为 .
的导函数y=f′(x)的部分图象如图所示,且导函数f'(x)的最小值为-2,则函数的表达式为 .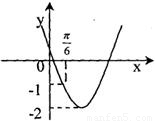 -1
-1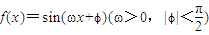 的导函数y=f'(x)的部分图象如图所示,且导函数f'(x)有最小值-2,则ω= ,ϕ= .
的导函数y=f'(x)的部分图象如图所示,且导函数f'(x)有最小值-2,则ω= ,ϕ= .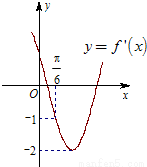
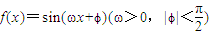 的导函数y=f′(x)的部分图象如图所示,且导函数f'(x)的最小值为-2,则函数的表达式为 .
的导函数y=f′(x)的部分图象如图所示,且导函数f'(x)的最小值为-2,则函数的表达式为 .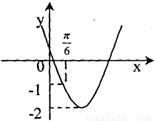 -1
-1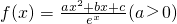 的导函数y=f'(x)的两个零点为-3和0.
的导函数y=f'(x)的两个零点为-3和0.