题目内容
9.在平面直角坐标系xOy中已知圆C:x2+(y-1)2=5,A为圆C与x轴负半轴的交点,过点A作圆C的弦AB,记线段AB的中点为M.若OA=OM,则直线AB的斜率为2.分析 因为圆的半径为$\sqrt{5}$,所以A(-2,0),连接CM,显然CM⊥AB,求出圆的直径,在三角形OCM中,利用正弦定理求出sin∠OCM,利用∠OCM与∠OAM互补,即可得出结论.
解答 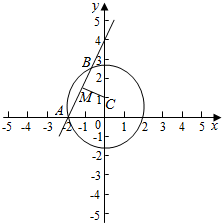 解:因为圆的半径为$\sqrt{5}$,所以A(-2,0),连接CM,显然CM⊥AB,
解:因为圆的半径为$\sqrt{5}$,所以A(-2,0),连接CM,显然CM⊥AB,
因此,四点C,M,A,O共圆,且AC就是该圆的直径,2R=AC=$\sqrt{5}$,
在三角形OCM中,利用正弦定理得2R=$\frac{OM}{sin∠OCM}$,
根据题意,OA=OM=2,
所以,$\sqrt{5}$=$\frac{2}{sin∠OCM}$,
所以sin∠OCM=$\frac{2}{\sqrt{5}}$,tan∠OCM=-2(∠OCM为钝角),
而∠OCM与∠OAM互补,
所以tan∠OAM=2,即直线AB的斜率为2.
故答案为:2.
点评 本题考查直线与圆的位置关系,考查正弦定理,考查学生的计算能力,属于中档题.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
14.顾客请一位工艺师把A,B两件玉石原料各制成一件工艺品.工艺师带一位徒弟完成这项任务.每件原料先由徒弟完成粗加工,再由工艺师进行精加工完成制作,两件工艺品都完成后交付顾客.两件原料每道工序所需时间(单位:工作日)如下:
则最短交货期为( )个工作日.
| 工序时间原料 | 粗加工 | 精加工 |
| 原料A | 9 | 15 |
| 原料B | 6 | 21 |
| A. | 36 | B. | 42 | C. | 45 | D. | 51 |
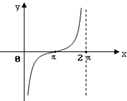
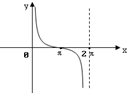
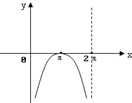
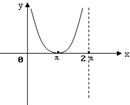
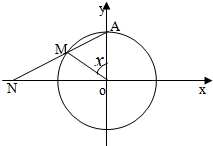 如图,圆x2+y2=1上一定点A(0,1),一动点M从A点开始逆时针绕圆运动一周,并记由射线OA按逆时针方向绕O点旋转到射线OM所形成的∠AOM为x,直线AM与X轴交于点N(t,0),则函数t=f(x)的图象大致为( )
如图,圆x2+y2=1上一定点A(0,1),一动点M从A点开始逆时针绕圆运动一周,并记由射线OA按逆时针方向绕O点旋转到射线OM所形成的∠AOM为x,直线AM与X轴交于点N(t,0),则函数t=f(x)的图象大致为( )