题目内容

12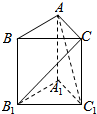．如图，在直三棱柱ABC-A1B1C1中，A1B1⊥A1C1，B1C⊥AC1，AB=2，AC=1，则该三棱柱的体积为（　　）
A．$\frac{1}{2}$B．1C．2D．4

分析 连结A1C，利用直线和平面垂直的判定和性质可得AC1⊥A1C，即四边形AA1C1C是正方形，从而求得该三棱柱的体积V=$\frac{1}{2}$•A1B1•A1C1 •AA1 的值．

解答 解：在直三棱柱ABC-A1B1C1中，连结A1C，∵A1B1⊥A1C1，∴A1B1⊥平面A1C，A1B1⊥AC1．
∵B1C⊥AC1，B1C∩A1C=C，∴AC1⊥平面A1B1C，∴AC1⊥A1C，
即四边形AA1C1C是正方形，∴AA1=AC=1，则该三棱柱的体积V=$\frac{1}{2}$•A1B1•A1C1 •AA1=$\frac{1}{2}$×1×2×1=1．
故选：B．

点评 本题主要考查直线和平面垂直的判定和性质，求得四边形AA1C1C是正方形，是解题的关键，属于基础题．

练习册系列答案
相关题目
16．将函数y=f（x）的图象上每一点的纵坐标缩小为原来的$\frac{1}{2}$倍，再将横坐标压缩为原来的$\frac{1}{2}$倍，再将整个图象沿x轴向左平移$\frac{π}{3}$，可得y=sinx，则原来的函数f（x）=2sin（$\frac{1}{2}$x-$\frac{π}{3}$）．
17．函数f（x）=x${\;}^{-\frac{1}{2}}$在区间[1，a]上的最小值是$\frac{\sqrt{2}}{2}$，则a=2．
14．已知函数f（x）=x-m-$\sqrt{1-x{\;}^{2}}$有两个零点，则实数m的取值范围是-$\sqrt{2}$＜m≤-1．
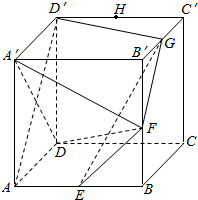7．在正方体ABCD-A′B′C′D′中，棱AB、BB′、B′C′、C′D′的中点分别是E，F，G，H，如图所示，则下列说法中正确的有（　　）
①点A，D′，H，F共面；
②直线EG与直线HF是异面直线；
③A′C⊥平面EFG；
④D′G∥平面A′DF．
A．①②B．②③C．②④D．③④
17．已知函数f（x）=$\frac{1}{2}$x2+lnx．
（1）求函数f（x）在区间[1，e]上的最大值、最小值；
（2）已知函数g（x）=ax2，a＞1，求证：在区间（1，+∞）上，f（x）＜g（x）．
4．已知函数f（x）=$\frac{lnx}{x}$，有下列四个命题：
p1：?x0∈R+，?x∈R+，f（$\frac{{x}_{0}+x}{2}$）＞$\frac{f（{x}_{0}）+f（x）}{2}$
p2：?x0∈R+，?x∈R+，f（$\frac{{x}_{0}+x}{2}$）＜$\frac{f（{x}_{0}）+f（x）}{2}$
p3：?x0∈R+，?x∈R+，f′（x0）＜$\frac{f（{x}_{0}+x）-f（{x}_{0}）}{x}$
p4：?x0∈R+，?x∈R+，f′（x0）＞$\frac{f（{x}_{0}+x）-f（{x}_{0}）}{x}$
其中的真命题是（　　）
A．p1，p2B．p1，p4C．p2，p3D．p2，p4
1．在△ABC中，b=asinC，c=acosB，则△ABC的形状是等腰直角三角形．．
2．已知函数f（x）=2ex+$\frac{1}{x}$，
（1）求f′（x）；
（2）求${∫}_{1}^{2}$f（x）dx．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网