题目内容
4.已知函数f(x)=$\frac{lnx}{x}$,有下列四个命题:p1:?x0∈R+,?x∈R+,f($\frac{{x}_{0}+x}{2}$)>$\frac{f({x}_{0})+f(x)}{2}$
p2:?x0∈R+,?x∈R+,f($\frac{{x}_{0}+x}{2}$)<$\frac{f({x}_{0})+f(x)}{2}$
p3:?x0∈R+,?x∈R+,f′(x0)<$\frac{f({x}_{0}+x)-f({x}_{0})}{x}$
p4:?x0∈R+,?x∈R+,f′(x0)>$\frac{f({x}_{0}+x)-f({x}_{0})}{x}$
其中的真命题是( )
| A. | p1,p2 | B. | p1,p4 | C. | p2,p3 | D. | p2,p4 |
分析 先求函数f(x)=$\frac{lnx}{x}$的定义域,再求导f′(x)=$\frac{1-lnx}{{x}^{2}}$,f″(x)=$\frac{2lnx-3}{{x}^{3}}$;从而由f″(x)=$\frac{2lnx-3}{{x}^{3}}$有正有负知p1假p2真,再由f(x)在(0,e)上是增函数,在[e,+∞)上是减函数知p3假,p3真.
解答 解:函数f(x)=$\frac{lnx}{x}$的定义域为(0,+∞),
f′(x)=$\frac{1-lnx}{{x}^{2}}$,f″(x)=$\frac{2lnx-3}{{x}^{3}}$;
∵f″(x)=$\frac{2lnx-3}{{x}^{3}}$有正有负,
∴p1:?x0∈R+,?x∈R+,f($\frac{{x}_{0}+x}{2}$)>$\frac{f({x}_{0})+f(x)}{2}$是假命题,
p2:?x0∈R+,?x∈R+,f($\frac{{x}_{0}+x}{2}$)<$\frac{f({x}_{0})+f(x)}{2}$是真命题;
∵当x∈(0,e)时,f′(x)>0,当x∈(e,+∞)时,f′(x)<0;
∴f(x)在(0,e)上是增函数,在[e,+∞)上是减函数,
故令x0=e,则f′(x0)=0,
且f(x0+x)<f(x0),
故f′(x0)>$\frac{f({x}_{0}+x)-f({x}_{0})}{x}$;
故p4:?x0∈R+,?x∈R+,f′(x0)>$\frac{f({x}_{0}+x)-f({x}_{0})}{x}$是真命题,
故选D.
点评 本题考查了导数的综合应用,同时考查了凸、凹函数的判断与应用,属于难题.

练习册系列答案
相关题目
8.若f(x+$\frac{1}{x}$)=x2+$\frac{1}{{x}^{2}}$+1,则函数f(x)的解析式为( )
| A. | f(x)=x2-1 | B. | f(x)=x2-1(x≥2) | ||
| C. | f(x)=x2-1(x≤-2) | D. | f(x)=x2-1(x≥2或x≤-2) |
12.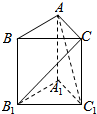 如图,在直三棱柱ABC-A1B1C1中,A1B1⊥A1C1,B1C⊥AC1,AB=2,AC=1,则该三棱柱的体积为( )
如图,在直三棱柱ABC-A1B1C1中,A1B1⊥A1C1,B1C⊥AC1,AB=2,AC=1,则该三棱柱的体积为( )
 如图,在直三棱柱ABC-A1B1C1中,A1B1⊥A1C1,B1C⊥AC1,AB=2,AC=1,则该三棱柱的体积为( )
如图,在直三棱柱ABC-A1B1C1中,A1B1⊥A1C1,B1C⊥AC1,AB=2,AC=1,则该三棱柱的体积为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
14.顾客请一位工艺师把A,B两件玉石原料各制成一件工艺品.工艺师带一位徒弟完成这项任务.每件原料先由徒弟完成粗加工,再由工艺师进行精加工完成制作,两件工艺品都完成后交付顾客.两件原料每道工序所需时间(单位:工作日)如下:
则最短交货期为( )个工作日.
| 工序时间原料 | 粗加工 | 精加工 |
| 原料A | 9 | 15 |
| 原料B | 6 | 21 |
| A. | 36 | B. | 42 | C. | 45 | D. | 51 |