题目内容
（2013•乌鲁木齐一模）设平面区域D是由双曲线y2-
=1的两条渐近线和抛物线y2=-8x的准线所围成的三角形（含边界与内部）．若点（x，y）∈D，则目标函数z=x+y的最大值为（ ）
| x2 | 4 |
分析：先求出双曲线的两条渐近线为y=±
x，抛物线y2=-8x的准线为x=2，结合图象可得 当直线y=-x+z过
点A（1，2）时，zmax=3，由此求得目标函数z=x+y的最大值．
| 1 |
| 2 |
点A（1，2）时，zmax=3，由此求得目标函数z=x+y的最大值．
解答：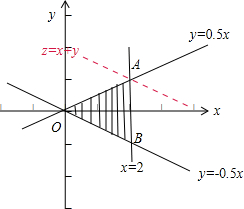
解：双曲线y2-
=1的两条渐近线为y=±
x，
抛物线y2=-8x的准线为x=2．
故可行域即图中阴影部分，（含边界）．
目标函数z=x+y中的z表示直线y=-x+z在y轴上的截距，
故当直线y=-x+z过点A（2，1）时，zmax=3，
故选D．
解：双曲线y2-| x2 |
| 4 |
| 1 |
| 2 |
抛物线y2=-8x的准线为x=2．
故可行域即图中阴影部分，（含边界）．
目标函数z=x+y中的z表示直线y=-x+z在y轴上的截距，
故当直线y=-x+z过点A（2，1）时，zmax=3，
故选D．
点评：本题主要考查抛物线、双曲线的标准方程，以及简单性质，简单的线性规划问题，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
（2013•乌鲁木齐一模）函数f（x）=2sin（ωx+φ）（ω＞0，0≤φ≤π）的部分图象如图所示，其 中A，B两点之间的距离为5，则f（x）的递增区间是（ ）