题目内容
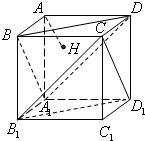 如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.有下列四个命题:
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.有下列四个命题:A.点H是△A1BD的垂心;
B.AH垂直平面CB1D1;
C.二面角C-B1D1-C1的正切值为
| 2 |
D.点H到平面A1B1C1D1的距离为
| 3 |
| 4 |
分析:结合正方体图形,逐一判断选项,求得结果即可.
解答:解:因为三棱锥A-A1BD是正三棱锥,故顶点A在底面的射映是底面中心,A正确;
面A1BD∥面CB1D1,而AH垂直平面A1BD,所以AH垂直平面CB1D1,B正确;
连接A1C1∩B1D1=O?∠COC1即为二面角C-B1D1-C1的平面角,tanα=
=
,C正确;
对于D,连接AC1,?AC1⊥面A1BD,故点H是AC1
的三等分点,故点H到平面A1B1C1D1的距离为
×AA1=
.从而D错.
则应填ABC.
面A1BD∥面CB1D1,而AH垂直平面A1BD,所以AH垂直平面CB1D1,B正确;
连接A1C1∩B1D1=O?∠COC1即为二面角C-B1D1-C1的平面角,tanα=
| 1 | ||||
|
| 2 |
对于D,连接AC1,?AC1⊥面A1BD,故点H是AC1
的三等分点,故点H到平面A1B1C1D1的距离为
| 2 |
| 3 |
| 2 |
| 3 |
则应填ABC.
点评:本题考查直线与平面垂直的判定,二面角及其度量等知识,考查空间想象能力,是基础题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
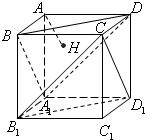
 (2010•湖北模拟)如图,正方体AC1的棱长为1,连接AC1,交平面A1BD于H,则以下命题中,错误的命题是( )
(2010•湖北模拟)如图,正方体AC1的棱长为1,连接AC1,交平面A1BD于H,则以下命题中,错误的命题是( )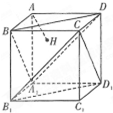 如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是( )
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是( )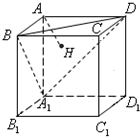 如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则点H到平面A1B1C1D1 的距离为
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则点H到平面A1B1C1D1 的距离为