题目内容
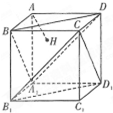 如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是( )
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是( )分析:利用直线AH和BB1所成角等于直线AH和AA1所成角,可得结论;连接正方体的体对角线AC1,则它在各面上的射影分别垂直于BD、A1B、A1D等,所以AC1⊥平面A1BD,则直线A1C与AH重合;面A1BD∥面CB1D1,而AH垂直平面A1BD,所以AH垂直平面CB1D1;因为三棱锥A-A1BD是正三棱锥,所以顶点A在底面的射影H是底面中心,故可得结论.
解答:解:直线AH和BB1所成角等于直线AH和AA1所成角,由于AA1=1,HA1=
,∴直线AH和BB1所成角不等于45°,故A错误;
连接正方体的体对角线AC1,则它在各面上的射影分别垂直于BD、A1B、A1D等,所以AC1⊥平面A1BD,则直线A1C与AH重合,所以选项B正确;
面A1BD∥面CB1D1,而AH垂直平面A1BD,所以AH垂直平面CB1D1,所以选项C正确;
因为三棱锥A-A1BD是正三棱锥,所以顶点A在底面的射影H是底面中心,所以选项D正确;
故选A.
| ||
| 3 |
连接正方体的体对角线AC1,则它在各面上的射影分别垂直于BD、A1B、A1D等,所以AC1⊥平面A1BD,则直线A1C与AH重合,所以选项B正确;
面A1BD∥面CB1D1,而AH垂直平面A1BD,所以AH垂直平面CB1D1,所以选项C正确;
因为三棱锥A-A1BD是正三棱锥,所以顶点A在底面的射影H是底面中心,所以选项D正确;
故选A.
点评:本题考查命题真假判断,考查正方体的性质,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
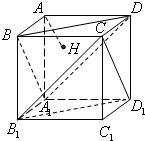 如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.有下列四个命题:
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.有下列四个命题: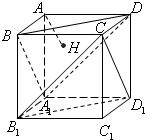
 (2010•湖北模拟)如图,正方体AC1的棱长为1,连接AC1,交平面A1BD于H,则以下命题中,错误的命题是( )
(2010•湖北模拟)如图,正方体AC1的棱长为1,连接AC1,交平面A1BD于H,则以下命题中,错误的命题是( )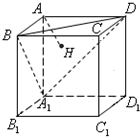 如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则点H到平面A1B1C1D1 的距离为
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则点H到平面A1B1C1D1 的距离为