题目内容
已知α为锐角,且 .
.(Ⅰ)求tanα的值;
(Ⅱ)求
 的值.
的值.
【答案】分析:(Ⅰ)通过正切的两角和公式可求tanα的值.
(Ⅱ)先把原式化简,再利用(Ⅰ)tanα的值求出sinα,得出答案.
解答:解:(Ⅰ)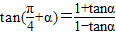
∴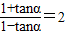 ,1+tanα=2-2tanα,
,1+tanα=2-2tanα,
∴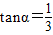
(Ⅱ)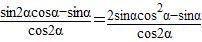 =
=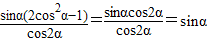
∵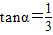 ,
,
∴cosα=3sinα,
又sin2α+cos2α=1,
∴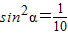
又α为锐角,
∴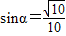 ,
,
∴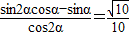
点评:本题主要考查用诱导公式化简求和.题中还出现了两角和公式、倍角公式等,要熟练掌握这些公式.
(Ⅱ)先把原式化简,再利用(Ⅰ)tanα的值求出sinα,得出答案.
解答:解:(Ⅰ)
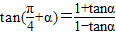
∴
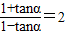 ,1+tanα=2-2tanα,
,1+tanα=2-2tanα,∴
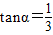
(Ⅱ)
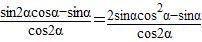 =
=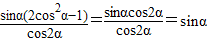
∵
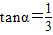 ,
,∴cosα=3sinα,
又sin2α+cos2α=1,
∴
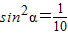
又α为锐角,
∴
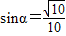 ,
,∴
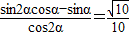
点评:本题主要考查用诱导公式化简求和.题中还出现了两角和公式、倍角公式等,要熟练掌握这些公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知α,β为锐角,且cosα=
,cosβ=
,则α+β的值是( )
| 1 | ||
|
| 1 | ||
|
A、
| ||
B、
| ||
C、
| ||
D、
|