题目内容
8. 如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.
如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.(1)证明EM⊥BF;
(2)请在图中作出平面ABC与平面BEF的交线(不要求证明)
(3)求平面BEF和平面ABC所成的锐二面角的正切值.
分析 (1)根据线面垂直得到线与线垂直,根据直径所对的圆周角是直角,得到两个三角形是等腰直角三角形,由线面垂直得到结果.
(2)做出辅助线,延长EF交AC于G,连BG,则BG即为所求交线.
(3)过C作CH⊥BG,连接FH.做出∠FHC为平面BEF与平面ABC所成的二面角的平面角,求出平面角.
解答  解:(1)证明:∵EA⊥平面ABC,BM?平面ABC,∴EA⊥BM.
解:(1)证明:∵EA⊥平面ABC,BM?平面ABC,∴EA⊥BM.
又∵BM⊥AC,EA∩AC=A,∴BM⊥平面ACFE,
而EM?平面ACFE,∴BM⊥EM.
∵AC是圆O的直径,∴∠ABC=90°.
又∵∠BAC=30°,AC=4,
∴AB=2$\sqrt{3}$,BC=2,AM=3,CM=1.
∵EA⊥平面ABC,FC∥EA,$\frac{FC}{EA}$=$\frac{1}{3}$,
∴FC⊥平面ABC.∴△EAM与△FCM都是等腰直角三角形.
∴∠EMA=∠FMC=45°.∴∠EMF=90°,即EM⊥MF,
∵MF∩BM=M,∴EM⊥平面MBF.
而BF?平面MBF,∴EM⊥BF.
(2)延长EF交AC于G,连BG,则BG即为平面ABC与平面BEF的交线.
(3)过C作CH⊥BG,连接FH.
由(1)知FC⊥平面ABC,BG?平面ABC,∴FC⊥BG.
而FC∩CH=C,∴BG⊥平面FCH.
∵FH?平面FCH,∴FH⊥BG,
∴∠FHC为平面BEF与平面ABC所成的二面角的平面角.
在Rt△ABC中,∵∠BAC=30°,AC=4,
∴BM=AB•sin30°=$\sqrt{3}$,
由$\frac{FC}{EA}$=$\frac{GC}{GA}$=$\frac{1}{3}$,得GC=2.
∵BG=$\sqrt{B{M}^{2}+M{G}^{2}}$=2$\sqrt{3}$,
又∵△GCH∽△GBM,
∴$\frac{GC}{BG}$=$\frac{CH}{BM}$,则CH=$\frac{GC•BM}{BG}$=$\frac{2•\sqrt{3}}{2\sqrt{3}}$=1.
∴△FCH是等腰直角三角形,∠FHC=45°,
∴平面BEF与平面ABC所成的锐二面角的余弦值为$\frac{\sqrt{2}}{2}$.
点评 本题主要考查空间点、线、面位置关系,二面角等基础知识,考查应用向量知识解决数学问题的能力,考查空间想象能力、运算能力和推理论证能力,注意解题方法的积累,属于中档题.

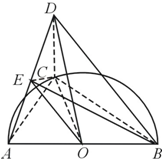 如图,已知点C是圆心为O半径为1的半圆弧上从点A数起的第一个三等分点,AB是直径,CD=1,CD⊥平面ABC,点E是AD的中点.
如图,已知点C是圆心为O半径为1的半圆弧上从点A数起的第一个三等分点,AB是直径,CD=1,CD⊥平面ABC,点E是AD的中点.