题目内容
(本小题满分12分)已知椭圆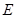 的对称轴为坐标轴,焦点在
的对称轴为坐标轴,焦点在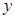 轴上,离心率
轴上,离心率 ,
,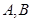 分别为椭圆的上顶点和右顶点,且
分别为椭圆的上顶点和右顶点,且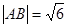 .
.
(Ⅰ)求椭圆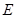 的方程;
的方程;
(Ⅱ)已知直线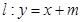 与椭圆
与椭圆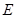 相交于
相交于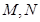 两点,且
两点,且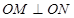 (其中
(其中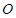 为坐标原点),求
为坐标原点),求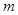 的值.
的值.
【答案】
(Ⅰ)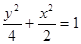 (Ⅱ)
(Ⅱ)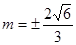
【解析】
试题分析:(1)设椭圆的方程为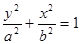 (
(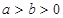 ),半焦距为
),半焦距为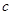 ,
,
由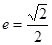 得,
得,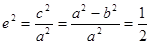 ,得
,得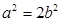 …………………………2分
…………………………2分
由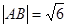 得,
得,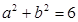 , ……………………………………………4分
, ……………………………………………4分
故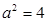 ,
,
所以,椭圆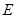 的方程为
的方程为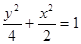 …………………………………………5分
…………………………………………5分
(2)由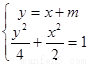 ,消去
,消去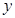 ,并整理得:
,并整理得: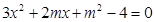 ,………7分
,………7分
由判别式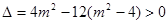 ,解得
,解得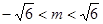 ………………8分
………………8分
设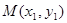 ,
,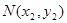 ,则
,则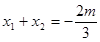 ,
,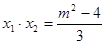 ……………10分
……………10分
由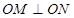 ,得
,得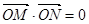 又
又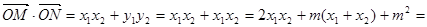
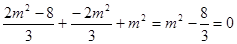 ,故
,故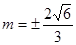 ………………………12分
………………………12分
考点:椭圆方程及直线与椭圆的位置关系
点评:直线与椭圆的位置关系通常联立方程利用韦达定理求解

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目