题目内容
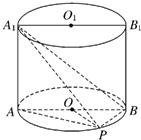 如图,已知点P在圆柱OO1的底面圆O上,AB、A1B1分别为圆O、圆O1的直径且A1A⊥平面PAB.
如图,已知点P在圆柱OO1的底面圆O上,AB、A1B1分别为圆O、圆O1的直径且A1A⊥平面PAB.(1)求证:BP⊥A1P;
(2)若圆柱OO1的体积V=12π,OA=2,∠AOP=120°,求三棱锥A1-APB的体积.
分析:(1)根据AP⊥BP与AA1⊥BP两个条件证明BP⊥平面PAA1,即可证明BP⊥A1P.
(2)根据题意求出S△PAB然后求出棱柱的高,即可求出体积.
(2)根据题意求出S△PAB然后求出棱柱的高,即可求出体积.
解答:证明:(1)证明:易知AP⊥BP,
由AA1⊥平面PAB,
得AA1⊥BP,
且AP∩AA1=A,
所以BP⊥平面PAA1,
故BP⊥A1P.
解:(2)由题意V=π•OA2•AA1=4π•AA1=12π,
解得AA1=3.
由OA=2,∠AOP=120°,得
∠BAP=30°,BP=2,AP=2
,
∴S△PAB=
×2×2
=2
,
∴三棱锥A1-APB的体积:
V=
S△PAB•AA1=
×2
×3=2
.
由AA1⊥平面PAB,
得AA1⊥BP,
且AP∩AA1=A,
所以BP⊥平面PAA1,
故BP⊥A1P.
解:(2)由题意V=π•OA2•AA1=4π•AA1=12π,
解得AA1=3.
由OA=2,∠AOP=120°,得
∠BAP=30°,BP=2,AP=2
| 3 |
∴S△PAB=
| 1 |
| 2 |
| 3 |
| 3 |
∴三棱锥A1-APB的体积:
V=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
点评:本题考查直线与平面垂直的判定,棱柱、棱锥、棱台的体积,考查数形结合、化归与转化的数学思想方法,通过对知识的综合考查,考查学生的综合运用能力.属于中档题.

练习册系列答案
相关题目
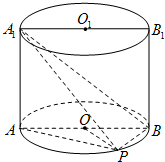 如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱OO1的表面积为20π,OA=2,∠AOP=120°.
如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱OO1的表面积为20π,OA=2,∠AOP=120°.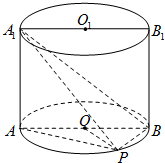 如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱OO1的表面积为24π,OA=2,∠AOP=120°.
如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱OO1的表面积为24π,OA=2,∠AOP=120°.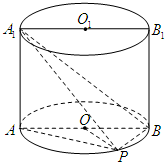 如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,OA=2,∠AOP=120°,三棱锥A1-APB的体积为
如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,OA=2,∠AOP=120°,三棱锥A1-APB的体积为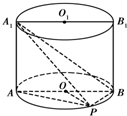 如图,已知点P在圆柱OO1的底面圆O上,AB、A1B1分别为圆O、O1的直径且A1A⊥平面PAB.
如图,已知点P在圆柱OO1的底面圆O上,AB、A1B1分别为圆O、O1的直径且A1A⊥平面PAB.