题目内容
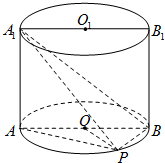 如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱OO1的表面积为24π,OA=2,∠AOP=120°.
如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱OO1的表面积为24π,OA=2,∠AOP=120°.(1)求三棱锥A1-APB的体积.
(2)求异面直线A1B与OP所成角的大小;(结果用反三角函数值表示)
分析:(1)由题意圆柱OO1的表面积为24π,OA=2,∠AOP=120°建立关于圆柱高的方程求出AA1=4,即得棱锥的高,再由,∠AOP=120°解出解出AP,进而解出BP,即可解出底面积,再棱锥的体积公式求体积即可;
(2)取AA1中点Q,连接OQ,PQ,可证得∠POQ或它的补角为异面直线A1B与OP所成的角,在三角形POQ中求异面直线所成的角即可.
(2)取AA1中点Q,连接OQ,PQ,可证得∠POQ或它的补角为异面直线A1B与OP所成的角,在三角形POQ中求异面直线所成的角即可.
解答:解:(1)由题意S表=2π•22+2π•2•AA1=24π,
解得AA1=4.(2分)
在△AOP中,OA=OP=2,∠AOP=120°,
所以AP=2
(3分)
在△BOP中,OB=OP=2,∠BOP=60°,
所以BP=2(4分)
VA1-APB=
S△APB•AA1(5分)
=
•
•2
•2•4=
(6分)
(2)取AA1中点Q,连接OQ,PQ,则OQ∥A1B,
得∠POQ或它的补角为异面直线A1B与OP所成的角.(8分)
又AP=2
,AQ=AO=2,得OQ=2
,PQ=4,(10分)
由余弦定理得cos∠POQ=
=-
,(12分)
得异面直线A1B与OP所成的角为arccos
.(14分)
解得AA1=4.(2分)
在△AOP中,OA=OP=2,∠AOP=120°,
所以AP=2
| 3 |
在△BOP中,OB=OP=2,∠BOP=60°,
所以BP=2(4分)
VA1-APB=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
8
| ||
| 3 |
(2)取AA1中点Q,连接OQ,PQ,则OQ∥A1B,
得∠POQ或它的补角为异面直线A1B与OP所成的角.(8分)
又AP=2
| 3 |
| 2 |
由余弦定理得cos∠POQ=
| PO2+OQ2-PQ2 |
| 2PO•OQ |
| ||
| 4 |
得异面直线A1B与OP所成的角为arccos
| ||
| 4 |
点评:本题考查了求三棱锥的体积与求两异面直线所成的角,在圆柱这一背景下,考查这两个问题方式比较新颖,解答本题关键是正确理解这些几何图形之间的位置关系的转化.

练习册系列答案
相关题目
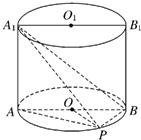 如图,已知点P在圆柱OO1的底面圆O上,AB、A1B1分别为圆O、圆O1的直径且A1A⊥平面PAB.
如图,已知点P在圆柱OO1的底面圆O上,AB、A1B1分别为圆O、圆O1的直径且A1A⊥平面PAB.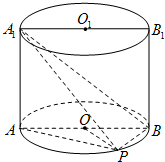 如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱OO1的表面积为20π,OA=2,∠AOP=120°.
如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱OO1的表面积为20π,OA=2,∠AOP=120°.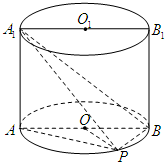 如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,OA=2,∠AOP=120°,三棱锥A1-APB的体积为
如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,OA=2,∠AOP=120°,三棱锥A1-APB的体积为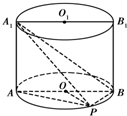 如图,已知点P在圆柱OO1的底面圆O上,AB、A1B1分别为圆O、O1的直径且A1A⊥平面PAB.
如图,已知点P在圆柱OO1的底面圆O上,AB、A1B1分别为圆O、O1的直径且A1A⊥平面PAB.