题目内容
【题目】已知 ![]() 函数
函数 ![]() 在区间
在区间 ![]() 上有1个零点;
上有1个零点; ![]() 函数
函数 ![]() 图象与
图象与 ![]() 轴交于不同的两点.若“
轴交于不同的两点.若“ ![]() ”是假命题,“
”是假命题,“ ![]() ”是真命题,求实数
”是真命题,求实数 ![]() 的取值范围.
的取值范围.
【答案】解:对于 ![]() 设
设 ![]() .
.
该二次函数图象开向上,对称轴为直线 ![]() ,
,
所以 ![]() ,所以
,所以 ![]() ;
;
对于 ![]() 函数
函数 ![]() 与
与 ![]() 轴交于不同的两点,
轴交于不同的两点,
所以 ![]() ,即
,即 ![]() ,
,
解得 ![]() 或
或 ![]() .
.
因为“ ![]() ”是假命题,“
”是假命题,“ ![]() ”是真命题,所以
”是真命题,所以 ![]() 一真一假.
一真一假.
①当 ![]() 真
真 ![]() 假时,有
假时,有 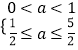 ,所以
,所以 ![]() ;
;
②当 ![]() 假
假 ![]() 真时,有
真时,有 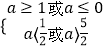 ,所以
,所以 ![]() 或
或 ![]() .
.
故答案为:实数 ![]() 的取值范围是
的取值范围是 ![]() .
.
【解析】对于命题p,二次函数的对称轴正好在区间的左端点处,则函数在区间中是增函数,要使函数有一个零点,则端点处函数值左负右正,求出a的范围;对于命题q,二次函数与x轴有两个交点,则判别式大于0,求出a的范围。由“ p ∧ q ”是假命题,“ p ∨ q ”是真命题,则p和q一真一假,分成p真q假和p假q真求出a的范围.

练习册系列答案
相关题目