题目内容
设函数 ,则有( )
,则有( )
A. 是奇函数, 是奇函数, | B. 是奇函数, 是奇函数, |
C. 是偶函数 是偶函数 | D. 是偶函数, 是偶函数, |
C
解析试题分析:因为函数表达式为 ,定义域为
,定义域为 ,所以
,所以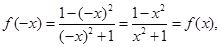 所以为偶函数;又
所以为偶函数;又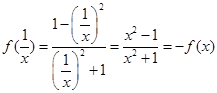 ,所以C正确.
,所以C正确.
考点:本小题主要考查函数奇偶性的判断以及函数表达式是否相等的判断.
点评:要考查函数的奇偶性,首先要考查函数的定义域是否关于原点对称.

练习册系列答案
相关题目
设偶函数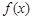 满足
满足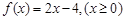 ,则不等式
,则不等式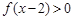 的解集是( )
的解集是( )
A.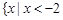 或 或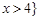 | B.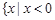 或 或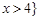 |
C.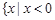 或 或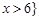 | D.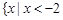 或 或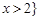 |
在下列函数中:①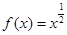 , ②
, ②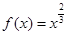 ,③
,③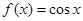 ,④
,④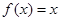 ,其中偶函数的个数是 ( )
,其中偶函数的个数是 ( )
| A.0 | B.1 | C.2 | D.3 |
函数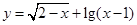 的定义域是 ( )
的定义域是 ( )
A.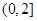 | B.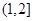 |
C.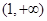 | D.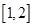 |
函数 ,若
,若 ,则
,则 的值为
的值为
| A.3 | B.0 | C.-1 | D.-2 |
若函数y=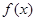 的图象经过(0,-1),则y=
的图象经过(0,-1),则y=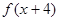 的反函数图象经过点( )
的反函数图象经过点( )
| A.(4,一1) | B.(一1,-4) | C.(-4,- 1) | D.(1,-4) |
函数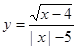 的定义域为( )z
的定义域为( )z
A.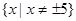 | B.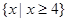 |
C.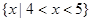 | D.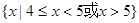 |
定义在R上的偶函数 满足:对任意的
满足:对任意的 ,有
,有 .则( )
.则( )
A. | B. |
C. | D. |
设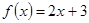 ,
, ,则
,则 等于( )
等于( )
| A.2x+1 | B.2x-1 | C.2x-3 | D.2x+7 |