题目内容
(本小题满分12分)
若函数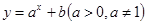 的图象过
的图象过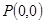 与
与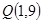 两点,设函数
两点,设函数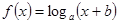 ;
;
(1)求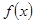 的定义域;
的定义域;
(2)求函数 的值域,判断g(x)奇偶性,并说明理由.
的值域,判断g(x)奇偶性,并说明理由.
【答案】
(1)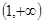 (2)
(2)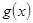 的值域为
的值域为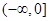 ,
,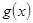 为偶函数
为偶函数
【解析】
试题分析(1)函数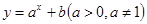 的图象过
的图象过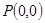 与
与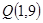 两点,
两点,
所以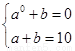 ,解得
,解得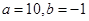 ; ……4分
; ……4分
所以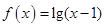 ,所以定义域为
,所以定义域为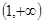 ; ……6分
; ……6分
(2)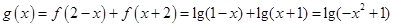 ,
,
所以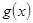 的定义域为
的定义域为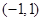 ,
,
而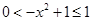 ,根据复合函数的单调性可知,
,根据复合函数的单调性可知,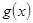 的值域为
的值域为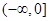 , ……9分因为
, ……9分因为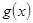 定义域关于原点对称,且满足
定义域关于原点对称,且满足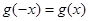 ,所以
,所以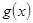 为偶函数. ……12分
为偶函数. ……12分
考点:本小题主要考查指数型函数和对数型函数,函数的定义域、值域、单调性和奇偶性.
点评:本小题综合求解函数的性质,重点考查函数的定义域、值域、单调性和奇偶性,要注意定义域和值域一定要写成集合或区间的形式,考查函数的奇偶性时,要先看函数的定义域是否关于原点对称.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目