Question

已知函数

(1)用定义证明函数f(x)在(－∞，＋∞)上为减函数；

(2)若x∈[1,2]，求函数f(x)的值域；

(3)若且当x∈[1,2]时g(x)≥0恒成立，求实数a的取值范围．

Answer 1

解析　(1)设x₁<x₂，则f(x₁)－f(x₂)＝

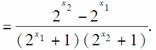
∴f(x₁)－f(x₂)>0即f(x₁)>f(x₂)．

∴f(x)在(－∞，＋∞)上为减函数．

(2)∵f(x)在(－∞，＋∞)上为减函数，

∴f(x)的值域为[－，－]．

(3)当x∈[1,2]时，g(x)∈[－，－]．

∵g(x)≥0在x∈[1,2]上恒成立，

∴－≥0，∴a≥.