题目内容
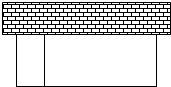
以墙为一边，用篱笆围成长方形的场地，并用平行于一边的篱笆隔开(如图2—6)．已知篱笆总长为定值l．
(1)写出场地面积y为一边长x的函数；
(2)指出函数的定义域；
(3)这块场地长宽各为多少时，场地的面积最大？最大值是多少？
答案：
解析：
解析：
解：(1)y＝x(l－3x) (2)0＜x＜
当3x＝l－3x即x＝ |
(3)y＝x(l－3x)＝ 
·3x·(l－3x)≤
．
时，即两边分别为
、
时面积最大为
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
