题目内容
(本小题满分12分)
已知椭圆的中心在坐标原点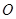 ,长轴长为
,长轴长为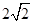 ,离心率
,离心率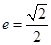 ,过右焦点
,过右焦点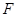 与
与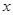 轴不垂直的直线
轴不垂直的直线 交椭圆于
交椭圆于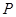 ,
,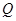 两点.
两点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)在线段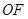 上是否存在点
上是否存在点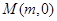 ,使得以
,使得以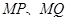 为
为
邻边的平行四边形是菱形? 若存在,求出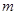 的取值范围;
的取值范围;
若不存在,请说明理由.
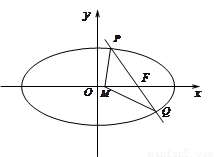
【答案】
(1) 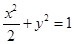
(2) 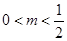
【解析】解:(Ⅰ)由已知,椭圆方程可设为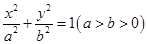 .
.
∵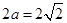 ,
,
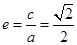 ,
,
∴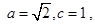
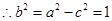 . 所求椭圆方程为
. 所求椭圆方程为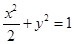 . ……………4分
. ……………4分
(Ⅱ)假设在线段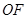 上存在点
上存在点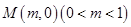 ,使得以
,使得以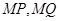 为邻边的平行四边形是菱形.因为直线与
为邻边的平行四边形是菱形.因为直线与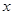 轴不垂直,所以设直线
轴不垂直,所以设直线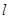 的方程为
的方程为 .
.
由 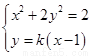 消去
消去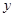 可得
可得 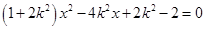 .
.
∴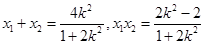 .
.
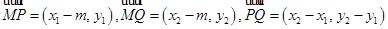 .其中
.其中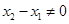
以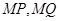 为邻边的平行四边形是菱形
为邻边的平行四边形是菱形
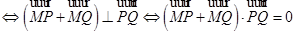
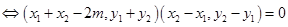
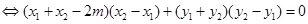
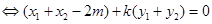
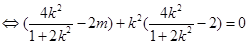
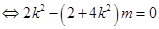
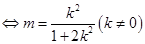 .
.
∴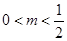 .
………………………12分
.
………………………12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目