题目内容
如图, 已知单位圆上有四点 , 分别设
, 分别设 的面积为
的面积为 .
.
(1)用 表示
表示 ;
;
(2)求 的最大值及取最大值时
的最大值及取最大值时 的值.
的值.
(1)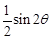 ,
,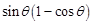
(2) 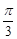
解析试题分析:解(1)根据三角函数的定义, 知 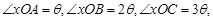
所以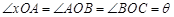 , 所
, 所 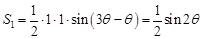 . 3分
. 3分
又因为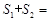 四边形OABC的面积=
四边形OABC的面积=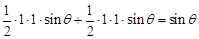 ,
,
所以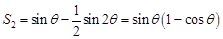 . 6分
. 6分
(2)由(1)知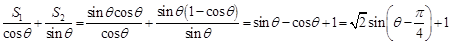 . 9分
. 9分
因为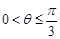 , 所以
, 所以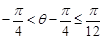 , 所以
, 所以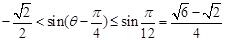 ,
,
所以 的最大值为
的最大值为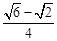 , 此时
, 此时 的值为
的值为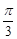 . 12分
. 12分
考点:三角函数的性质
点评:主要是考查了三角函数的性质以及二倍角公式的运用,属于基础题。

练习册系列答案
相关题目
已知某海滨浴场的海浪高达y(米)是时间t(0≤t≤24,单位:小时)的函数,记作y=f(t).下表是某日各时的浪高数据.
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T、振幅A及函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8:00至晚上20:00之间,有多长时间可供冲浪者进行运动?
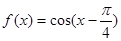 .
.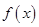 在区间
在区间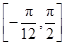 上的最大值和最小值;
上的最大值和最小值;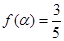 ,其中
,其中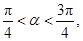 求
求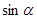 的值.
的值.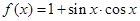 .(1)求函数
.(1)求函数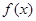 的最小正周期和最小值;(2)若
的最小正周期和最小值;(2)若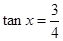 ,
,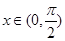 ,求
,求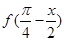 的值.
的值. ,
, 在
在 上的最大值与最小值;
上的最大值与最小值; 使得
使得 对任意
对任意 恒成立,求
恒成立,求 的值.
的值. 的一段图象如图所示.
的一段图象如图所示.
 的解析式;
的解析式; 个单位,得到
个单位,得到 的图象,求直线
的图象,求直线 与函数
与函数 的图象在
的图象在 内所有交点的坐标.
内所有交点的坐标.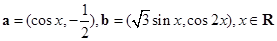 , 设函数
, 设函数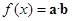 .
.  上的最大值和最小值.
上的最大值和最小值.  .
. 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;  ,求
,求 的值.
的值.  ,D为海岸线l上的一点.设CD=xkm(x>
,D为海岸线l上的一点.设CD=xkm(x> ),点D对跑道AB的视角为
),点D对跑道AB的视角为 .
.