题目内容
解下列不等式（1）x2-3x-10＜0
（2）（x-4）（x+2）≤7
（3）x2+x-1＞0
（4）2x2-3x+5＜0
（5）|3x+5|+1＞6
（6）|x+1|+|x-2|≥5．
分析：前四个不等式都是二次不等式，直接求解即可，后两个不等式是绝对值不等式，先去掉绝对值符号，然后求解即可．
解答：解：（1）x2-3x-10＜0的解集为{x|-2＜x＜5}
（2）（x-4）（x+2）≤7可化为：x2-2x-15≤0，它的解集为{x|-3＜x＜5}
（3）x2+x-1＞0它的解集为{x|x＜
或x＞
}
（4）2x2-3x+5＜0因为△＜0，所以它的解集为∅
（5）|3x+5|+1＞6转化为：|x+
| ＞
所以根据绝对值的几何意义，它的解集为{x|0＜x或x＜-5}
（6）|x+1|+|x-2|≥5．根据绝对值的几何意义，它的解集为{x|4≤x或x≤-3}
（2）（x-4）（x+2）≤7可化为：x2-2x-15≤0，它的解集为{x|-3＜x＜5}
（3）x2+x-1＞0它的解集为{x|x＜
-1-
| ||
| 2 |
-1+
| ||
| 2 |
（4）2x2-3x+5＜0因为△＜0，所以它的解集为∅
（5）|3x+5|+1＞6转化为：|x+
| 5 |
| 3 |
| 5 |
| 3 |
（6）|x+1|+|x-2|≥5．根据绝对值的几何意义，它的解集为{x|4≤x或x≤-3}
点评：本题是基础题，考查二次不等式的求法，注意判别式的应用，绝对值不等式的求法，注意绝对值的几何意义的应用，考查计算能力．
练习册系列答案
相关题目
＞x－1；(2)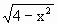
＞－x－1．