题目内容
解下列不等式
(1)
>
(2)(2x-5)(x-3)(x-4)≥0.
(1)
| x-1 |
| x-2 |
| 1 |
| 2 |
(2)(2x-5)(x-3)(x-4)≥0.
分析:(1)由
>
可得
>0,即x(x-2)>0,由此求得不等式的解集.
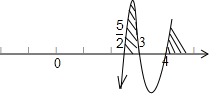
(2)由(2x-5)(x-3)(x-4)≥0,用穿根法求得它的解集.
| x-1 |
| x-2 |
| 1 |
| 2 |
| x |
| 2(x-2) |
(2)由(2x-5)(x-3)(x-4)≥0,用穿根法求得它的解集.
解答:解:(1)由
>
可得
>0,即x(x-2)>0,
解得 x<0,或x>2,故不等式的解集为(-∞,0)∪(2,+∞).
(2)由(2x-5)(x-3)(x-4)≥0,用穿根法求得它的解集为[
,3]∪[4,+∞).
| x-1 |
| x-2 |
| 1 |
| 2 |
| x |
| 2(x-2) |
解得 x<0,或x>2,故不等式的解集为(-∞,0)∪(2,+∞).
(2)由(2x-5)(x-3)(x-4)≥0,用穿根法求得它的解集为[
| 5 |
| 2 |

点评:本题主要考查分式不等式、高次不等式的解法,属于中档题.

练习册系列答案
相关题目
 >x-1;(2)
>x-1;(2)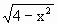 >-x-1.
>-x-1.