题目内容
函数f(x)=-x2+2x+8,则下列说法正确的是( )A.f(x)是增函数 B.f(x)在(-∞,1)上是增函数
C.f(x)是减函数 D.f(x)在(-∞,1)上是减函数
思路解析:本题是已知函数解析式确定单调区间的典型题.由于函数f(x)=-x2+2x+8是二次函数,所以在整个定义内不是严格单调函数.在对称轴的两侧是严格单调的.因此解答此题的关键是确定对称轴.根据二次函数对称轴的公式x=-![]() 可求.
可求.
解法一:(综合法)依题意得函数f(x)=-x2+2x+8的对称轴方程为x=-![]() =1,又因为二次项系数为-1<0,所以开口方向向下.所以f(x)在(-∞,1)上是增函数,在(1,+∞)上是减函数.因此,选B.
=1,又因为二次项系数为-1<0,所以开口方向向下.所以f(x)在(-∞,1)上是增函数,在(1,+∞)上是减函数.因此,选B.
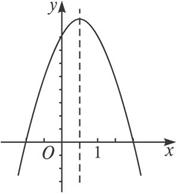
解法二:(数形结合法,图象法)如图所示,便知f(x)在(-∞,1)上是增函数.因此,选B.
解法三:(求导法)f′(x)=-2x+2>0,解得x<1,即f(x)在(-∞,1)上是增函数,f′(x)=-2x+2<0,解得x>1,即f(x)在(1,+∞)上是减函数.因此,选B.
答案:B

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=
若f(2-a2)>f(a),则实数a的取值范围是( )
|
| A、(-∞,-1)∪(2,+∞) |
| B、(-1,2) |
| C、(-2,1) |
| D、(-∞,-2)∪(1,+∞) |