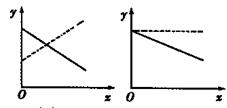题目内容
已知函数f(x)=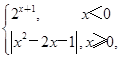 ,若方程f(x)+2a-1=0恰有4个实数根,则实数a的取值范围是 ( )
,若方程f(x)+2a-1=0恰有4个实数根,则实数a的取值范围是 ( )
A.(-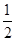 ,0 ] ,0 ] | B.[-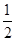 ,0 ] ,0 ] |
C.[1,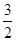 ) ) | D.(1,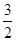 ] ] |
A
解析试题分析:方程 恰有四个实数根,等价于函数
恰有四个实数根,等价于函数 与函数
与函数 的图象恰有四个不同的交点,在同一坐标系中画出函数
的图象恰有四个不同的交点,在同一坐标系中画出函数 与函数
与函数 的图象如下:
的图象如下:
由图可知,当 时,即
时,即 时,两图象恰有四个不同的交点,所以答案选A.
时,两图象恰有四个不同的交点,所以答案选A.
考点:1、函数的图象;2、数形结合的思想.

练习册系列答案
相关题目
已知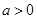 且
且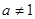 ,函数
,函数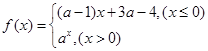 满足对任意实数
满足对任意实数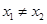 ,都有
,都有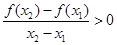 成立,则
成立,则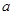 的取值范围是 ( )
的取值范围是 ( )
A.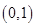 | B.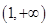 | C.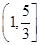 | D.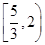 |
函数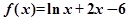 的零点一定位于区间( )
的零点一定位于区间( )
A.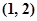 | B.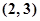 | C.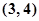 | D.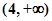 |
设函数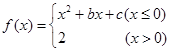 ,若
,若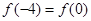 ,
,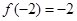 ,则关于
,则关于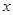 的方程
的方程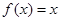 的解的个数为 ( )
的解的个数为 ( )
| A.1 | B.2 | C.3 | D.4 |
函数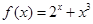 的零点所在区间为( )
的零点所在区间为( )
A.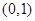 | B. | C.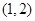 | D.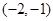 |
已知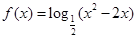 的单调递增区间是( )
的单调递增区间是( )
A.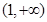 | B.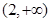 | C.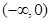 | D. |
下列函数中,在定义域内是单调递增函数的是( )
A.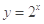 | B.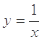 | C.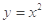 | D. |
函数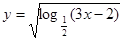 的定义域是( )
的定义域是( )
A.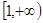 | B.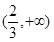 | C.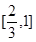 | D.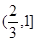 |
 ,另一种平均价格曲线
,另一种平均价格曲线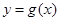 ,如
,如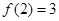 表示股票开始买卖后2小时的即时价格为3元;
表示股票开始买卖后2小时的即时价格为3元;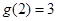 表示2小时内的平均价格为3元.下面给出了四个图像,实线表示
表示2小时内的平均价格为3元.下面给出了四个图像,实线表示